19. 数据结构篇：堆

什么是堆

堆(Heap) 是一种特殊的树，它必须满足以下条件：

• 堆是一颗完全二叉树
• 堆中每个节点都必须大于等于(或小于等于) 其子树中每个节点的值

其中，每个节点都大于等于子树节点的叫做“大顶堆”，每个节点都小于等于其子树节点的叫做“小顶堆”。

堆的存储

堆是一个完全二叉树，最适合用数组来存储。

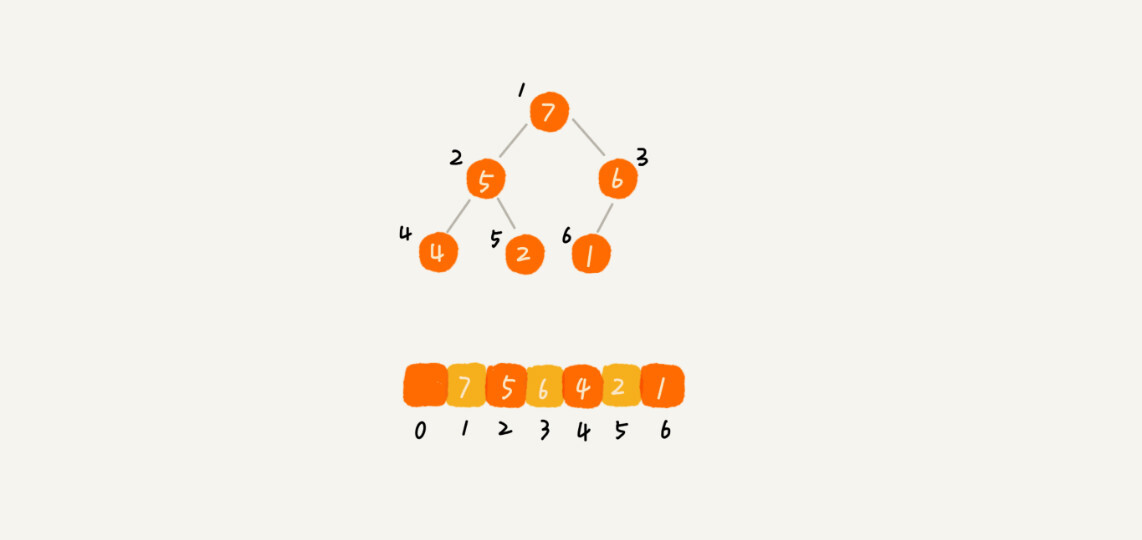
为了方便计算，一般从数组下标 1 开始存储，下标 i 的左子节点的下标为 i * 2，右子节点的下标为 i *2 + 1，父节点的下标为 i/2 取整(i > 1)。

堆化过程

1. 往堆中插入一个元素

先把插入的元素放到堆的最后，然后将新插入的节点与父节点对比大小，如果小于(或大于)父节点，就互换两个节点，一直重复这个过程，直到父节点满足堆的大小关系。这个过程叫 从下往上堆化。

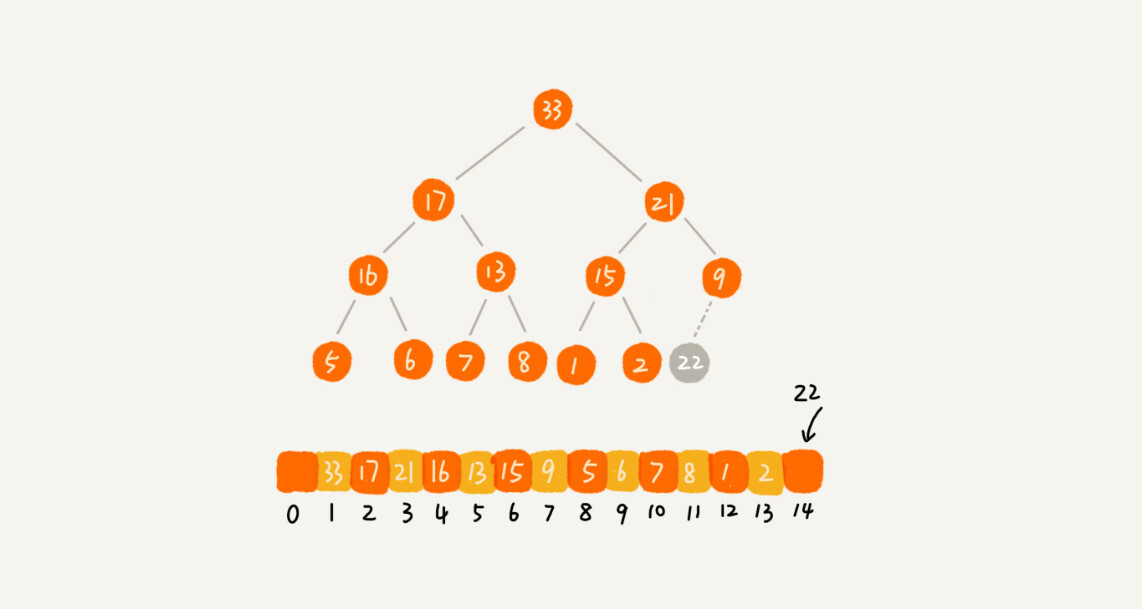
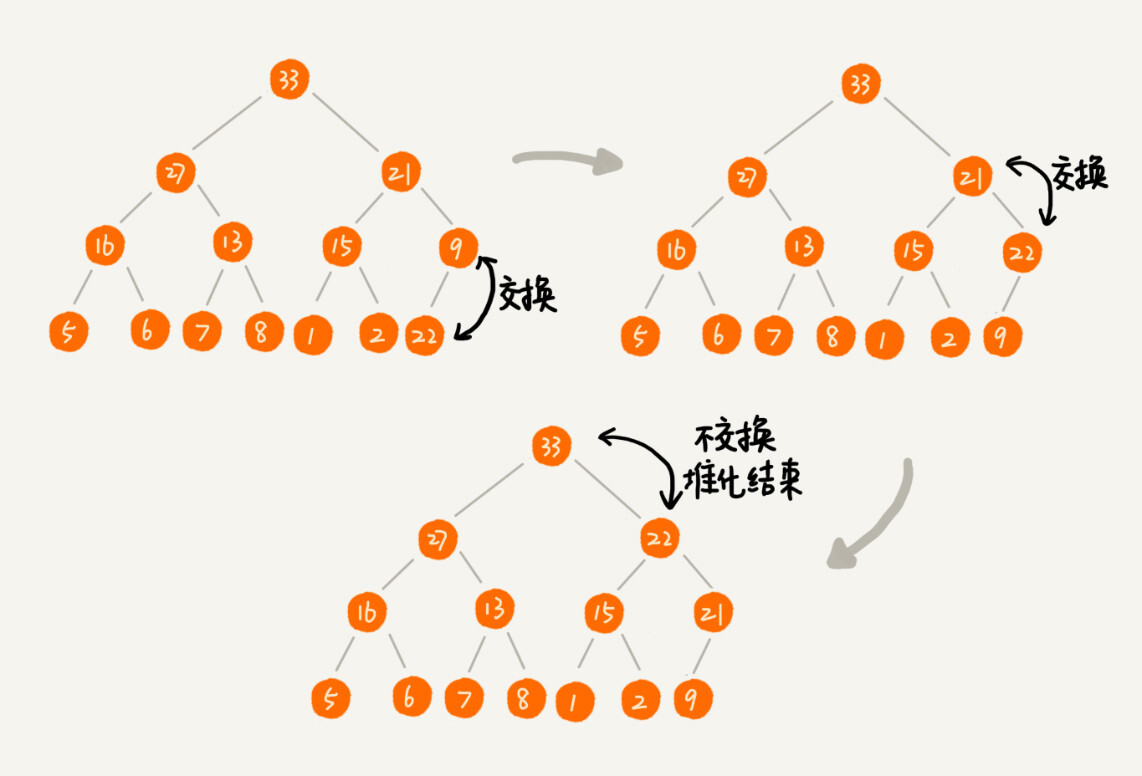
2. 删除堆顶元素

假设构造的是大顶堆，堆顶元素就是最大的元素。当删除一个堆顶元素时，需要找出第二大元素放到堆顶。过程如下：

先把最后一个节点放到堆顶，然后和父子节点比较大小，对于不满足父子节点大小关系的，互换两个节点，重复此过程，知道父子节点的关系满足大小为止。这是从上往下堆化的过程。

3. 堆化的时间复杂度

堆化是顺着节点所在路径比较交换的操作，所以堆化的时间复杂度跟树的高度成正比。一个包含 n 的节点的完全二叉树，高度不会超过 log₂n，所以堆化的时间复杂度为 O(logn)。

堆排序

堆排序的过程分为两步：建堆和排序。

建堆就是先将要排序的数据变成一个堆，有两种思路：

1. 遍历数组数据，将数据一个个插入堆中(注：初始化堆只有一个数据) 进行堆化；
2. 将数据从后往前处理数组，并且从上往下进行堆化。因为叶子节点往下堆化只能自己跟自己比较，所以可以直接从第一个非叶子节点开始，依次进程堆化就可以了。

第二中思路比较巧妙，可以减少节点的堆化，因为叶子节点的数据都是 n/2 +1 ~ n 的节点，所以第一个非叶子节点的位置为 n/2 ，只需要对下标为 n/2 到 1 的数据进行堆化。

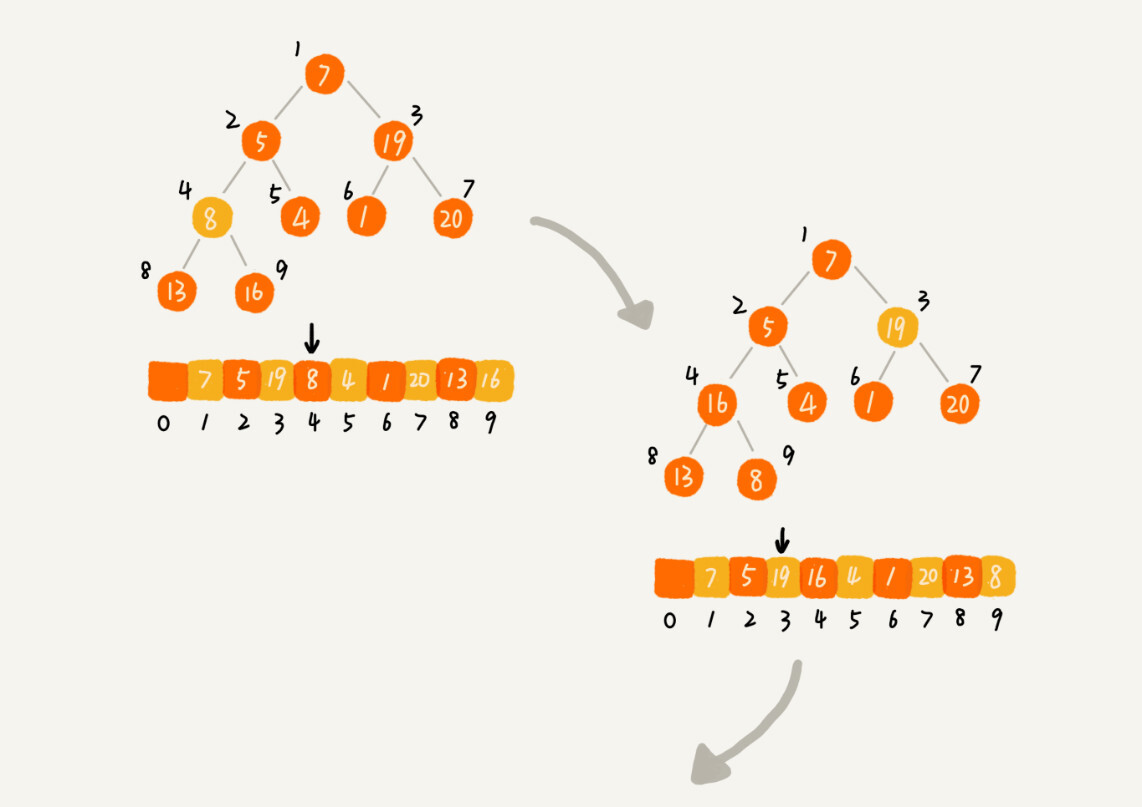
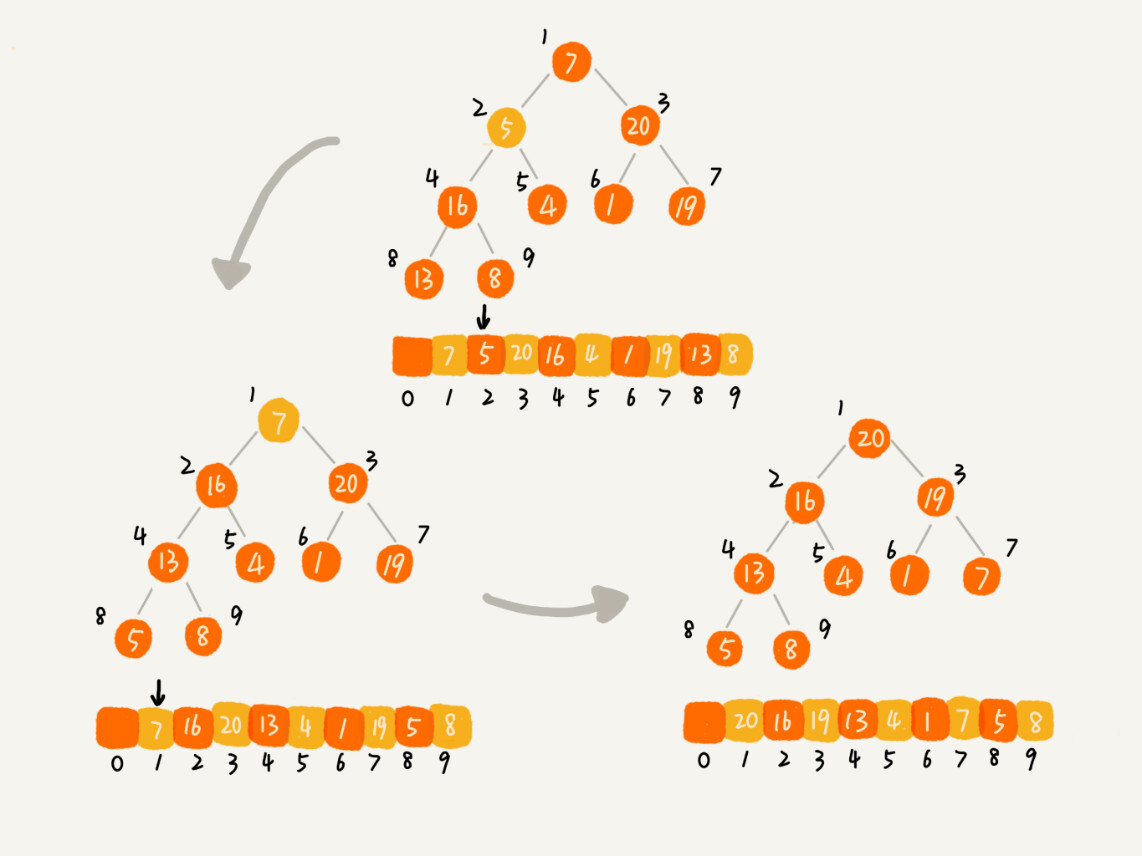
建堆结束后，就可以进行排序了。

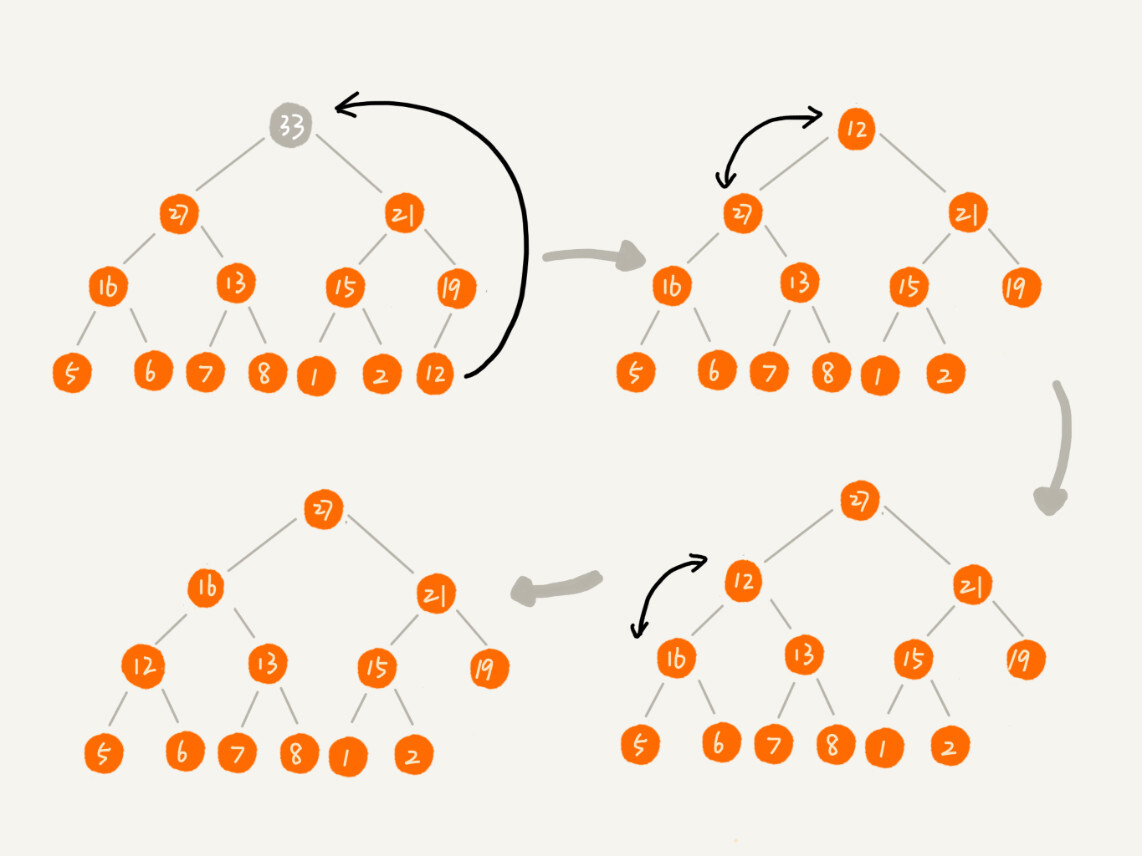
数组中的数据已经按照大顶堆的特性来组织了，数组中的第一个元素就是堆顶，把它跟数组的最后一个元素交换，最大元素就放到了下标为 n 的位置。类似删除了堆顶元素，然后把 n -1 个元素组织成堆，重复把堆顶元素放到 n -1 的位置，重复此过程，直到最后堆中只剩下一个元素，排序就完成了。

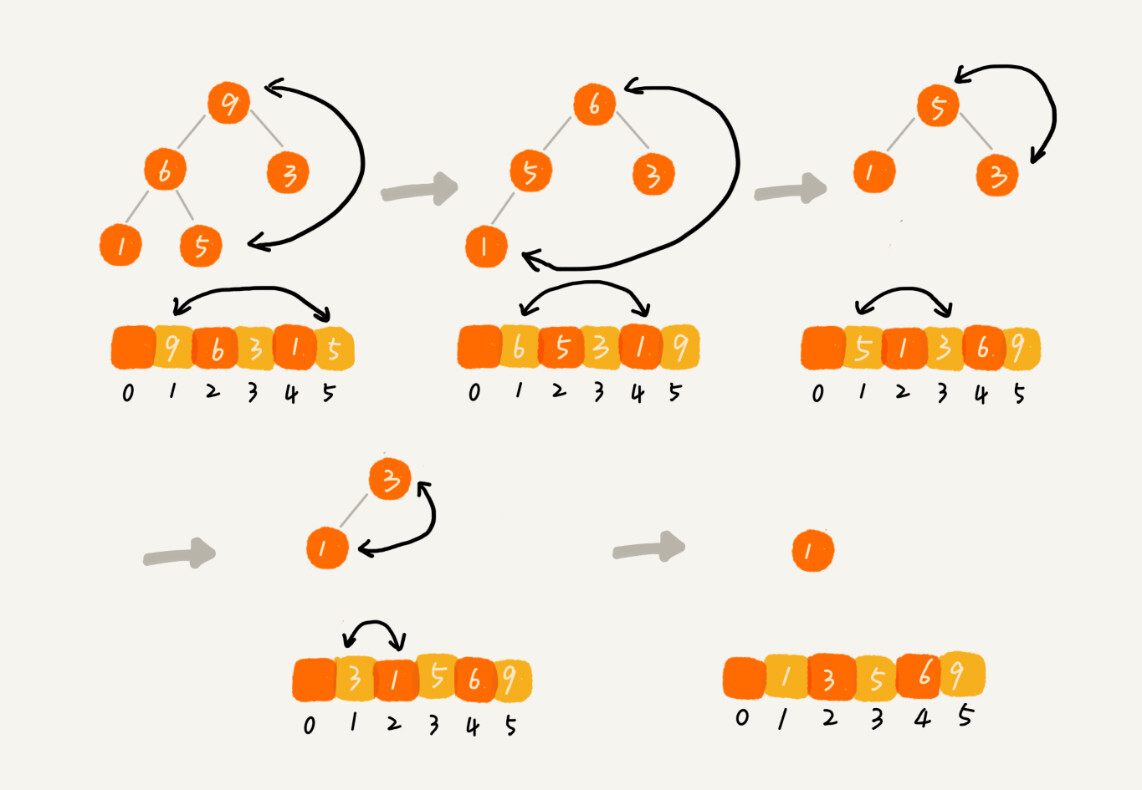
建堆过程的时间复杂度为 O(n) ，排序过程的时间复杂度为 O(nlogn)，所以整体的时间复杂度为两者之和。

 

关注微信公众账号「曹当家的」，订阅最新文章推送