6. 数据结构篇:栈
定义
栈是一种操作受限的线性表结构,只允许在一端插入和删除数据。具有先进后出,后进先出的特性。可以想象成一叠盘子,每次只能从最上面取 
实现
栈可以用数组来实现,也可以用链表来实现。用数组实现的叫顺序栈,用链表实现的叫链式栈。
栈主要是要实现入栈和出栈的功能。下面用 Python 来分别实现一个顺序栈和链式栈:
顺序栈:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# created on '2019/1/20'
class ArrayStack():
"""基于数组实现的顺序栈"""
def __init__(self, n: int):
self.arr = []
self.count = 0
self.n = n
def push(self, item):
if self.count == self.n:
print(' 栈溢出了 ', self.arr)
return False
self.arr.append(item)
self.count += 1
print('push 操作:', self.arr)
return True
def pop(self):
if self.count == 0:
print(' 栈空了 ', self.count)
return None
item = self.arr[-1]
self.arr = self.arr[:-1]
self.count -= 1
print('pop 操作:', item)
return item
def __repr__(self):
return "{}".format(self.arr)
if __name__ == '__main__':
A = ArrayStack(10)
A.push(3)
A.push(1)
A.push(4)
print(A)
A.pop()
A.pop()
A.pop()
A.pop() #栈空了,返回 None
print(A)
链式栈:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# created on '2019/1/20'
class Node():
"""链表结点和 next 指针"""
def __init__(self, data, next=None):
self.data = data
self.next = next
class LinkedStack():
"""基于链表实现的栈"""
def __init__(self):
self.base_node = None
def push(self, item):
new_node = Node(item)
new_node.next = self.base_node
self.base_node = new_node
def pop(self):
if self.base_node:
item = self.base_node.data
self.base_node = self.base_node.next # 表示删除一个结点
def __repr__(self):
base_node = self.base_node
nums = []
while base_node:
nums.append(base_node.data)
base_node = base_node.next
return "->".join(str(item) for item in items)
if __name__ == '__main__':
stack = LinkedStack()
stack.push(1)
stack.push(2)
stack.push(3)
stack.push(4)
stack.pop()
print(stack) # 3->2->1
分析一下很容易得出,不管是出栈还是入栈操作,时间复杂度都为 O(1)。
应用
栈在函数调用中的作用
在计算机中,函数调用是通过栈(stack)这种数据结构实现的,每当进入一个函数调用,栈就会加一层栈帧,每当函数返回,栈就会减一层栈帧。
栈在表达式求值中的应用
编译器是通过两个栈来进行表达式的加减乘除操作的,一个栈 A 用来保存操作数,一个栈 B 用来保存操作符。
计算时,从左到右遍历表达式,当遇到数字就直接入栈 A,当遇到操作符就与栈 B 的栈顶操作符进行比较,如果比栈顶操作符优先级高就直接入栈,如果比栈顶操作符优先级低或者相同,就从运算符栈中取栈顶运算符,从操作数栈的栈顶取 2 个操作数,然后进行计算,再把计算完的结果压入操作数栈,继续比较。
如:3+5*8-6 这个表达式的计算过程: 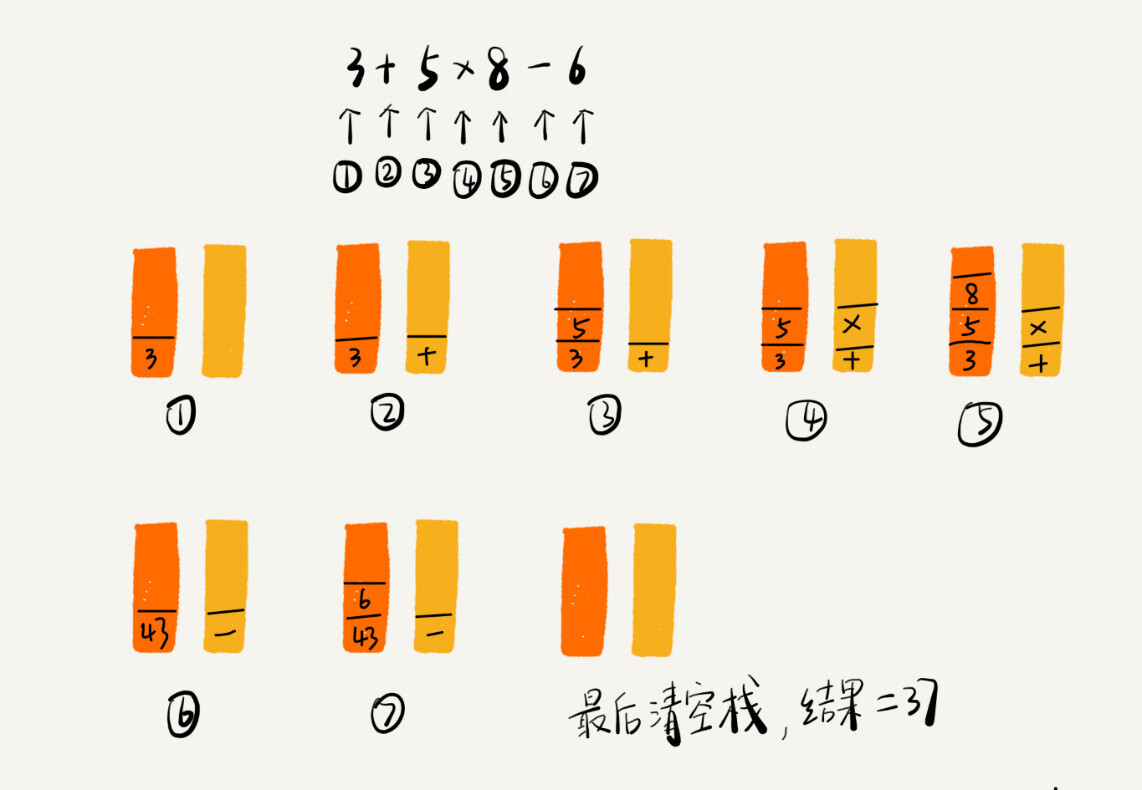
栈在括号匹配中的应用
我们假设表达式中只包含三种括号,圆括号 ()、方括号 [] 和花括号 {},并且它们可以任意嵌套。比如,{[{}]}或 [{()}([])] 等都为合法格式,而{[}()] 或 [({)] 为不合法的格式。那我现在给你一个包含三种括号的表达式字符串,如何检查它是否合法呢?
这里也可以用栈来解决。我们用栈来保存未匹配的左括号,从左到右依次扫描字符串。当扫描到左括号时,则将其压入栈中;当扫描到右括号时,从栈顶取出一个左括号。如果能够匹配,比如“(”跟“)”匹配,“[”跟“]”匹配,“{”跟“}”匹配,则继续扫描剩下的字符串。如果扫描的过程中,遇到不能配对的右括号,或者栈中没有数据,则说明为非法格式。
当所有的括号都扫描完成之后,如果栈为空,则说明字符串为合法格式;否则,说明有未匹配的左括号,为非法格式。
栈在浏览器前进后退功能中的作用
如何实现浏览器的前进、后退功能?
可以用两个栈 X、Y 来完美解决这个问题。
当顺序浏览了 a,b,c 三个页面,就依次把 a,b,c 压入栈 X 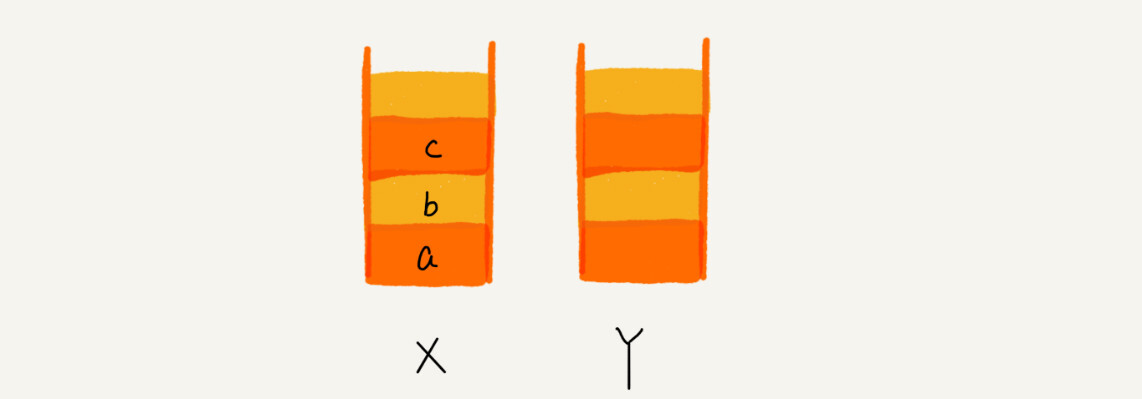
当点击浏览器后退按钮,从页面 c 后退到页面 a,就依次把 c,b 取出放入 Y 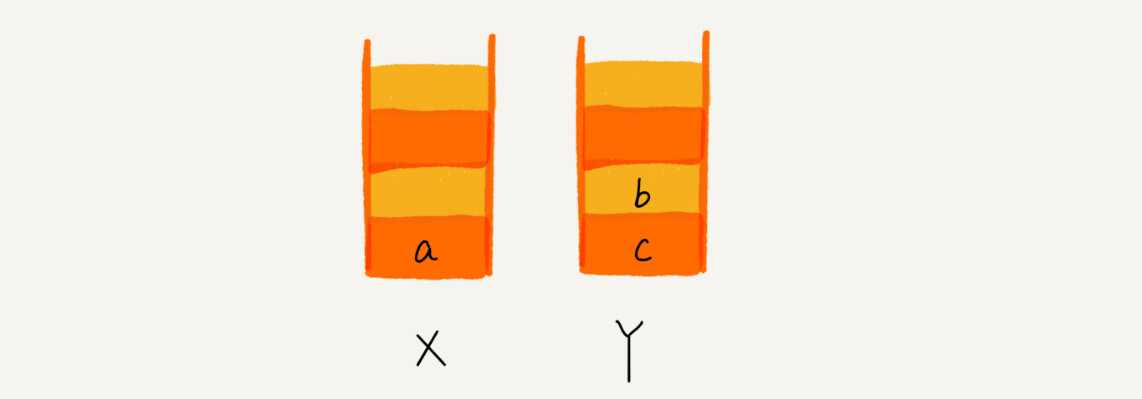
这是如果想看页面 b,就点击前进按钮,把 b 从栈 Y 中弹出放入 X 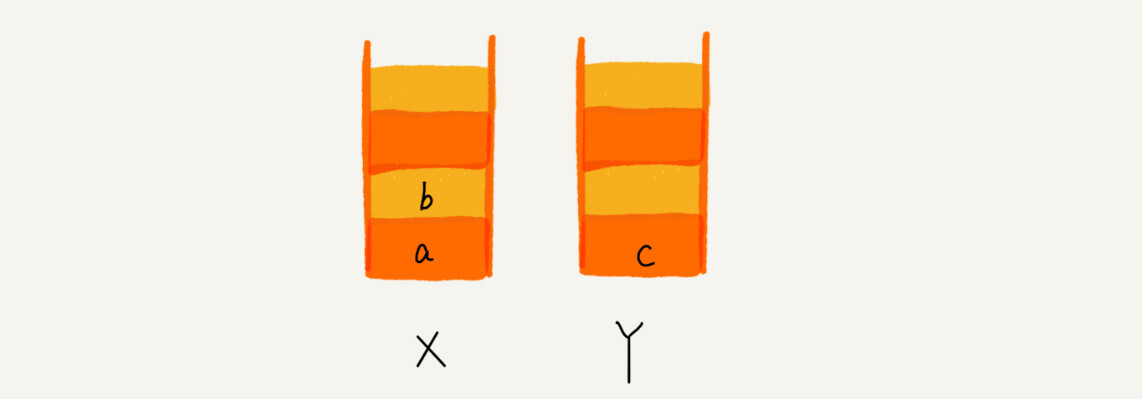
这时候如果新开了一个页面 d,页面 c 就无法再通过前进后退访问了,所以需要清空栈 Y 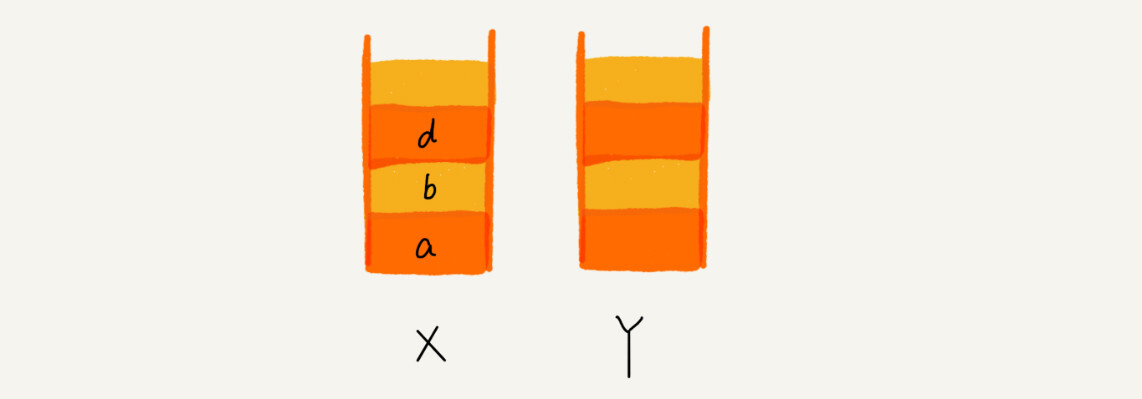
本文首发于 turbobin’s Blog 。转载请注明出处,附上本原文链接, 谢谢合作。

关注微信公众账号「曹当家的」,订阅最新文章推送