18. 数据结构篇：递归树

递归树

如果把递归过程一层一层分解，其实可以变成一颗树，即递归树。

借助递归树，可以比较容易的分析递归算法的时间复杂度。

斐波那契递归树

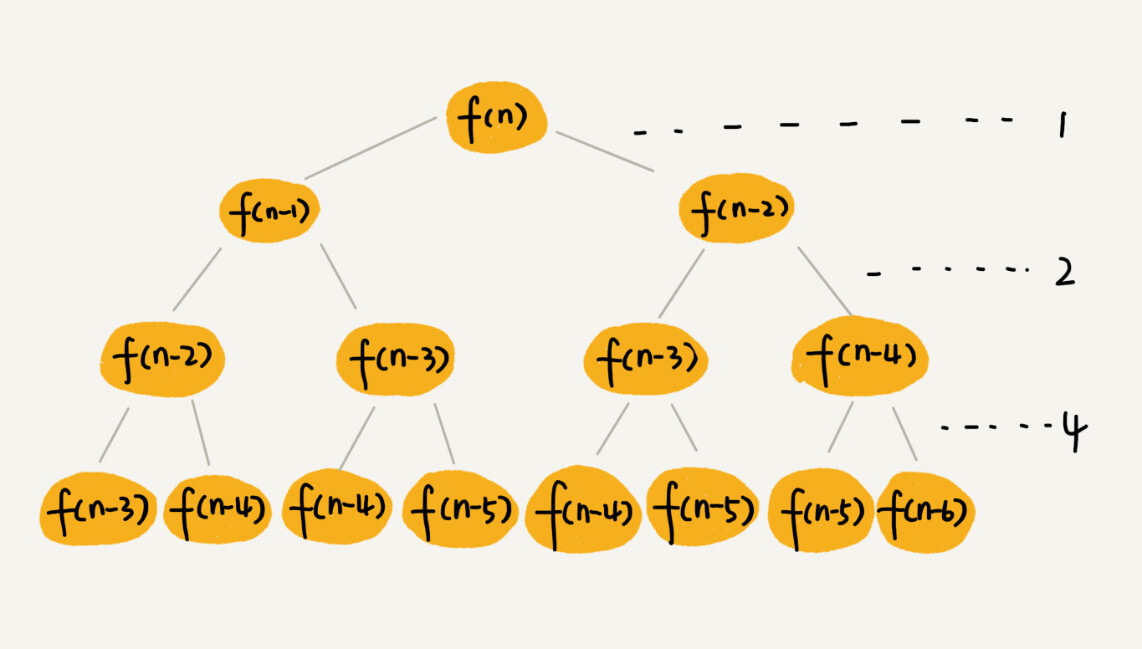
f(n) 分解为 f(n-1) 和 f(n-2)，每次数据的规模都是 -1 或 -2，叶子节点的数据规模是 1 或者 2，所以，从根节点到叶子节点，每条路径的长短都不一样。不过可以求出最短和最长路径：如果每次都是 f(n-1)，那么最长路径就是 n，如果每次都是 f(n-2)，那么最短路径是 n/2。

每一次分解的合并操作都要做一次加法运算，假设时间消耗为 1，那么第一层的总时间消耗为 1，第二层的总时间消耗为 2，第 3 层为 4，……，第 k 层的时间总消耗为 2^k-1 。

如果路径长度为 n，则总时间消耗为 2^n -1

如果路径长度为 n/2，则算法的总时间消耗为 2^n/2 - 1。

所以斐波那契算法的时间复杂度介于 O(2^n -1) 和 O(2^n/2) 之间。

归并排序递归树

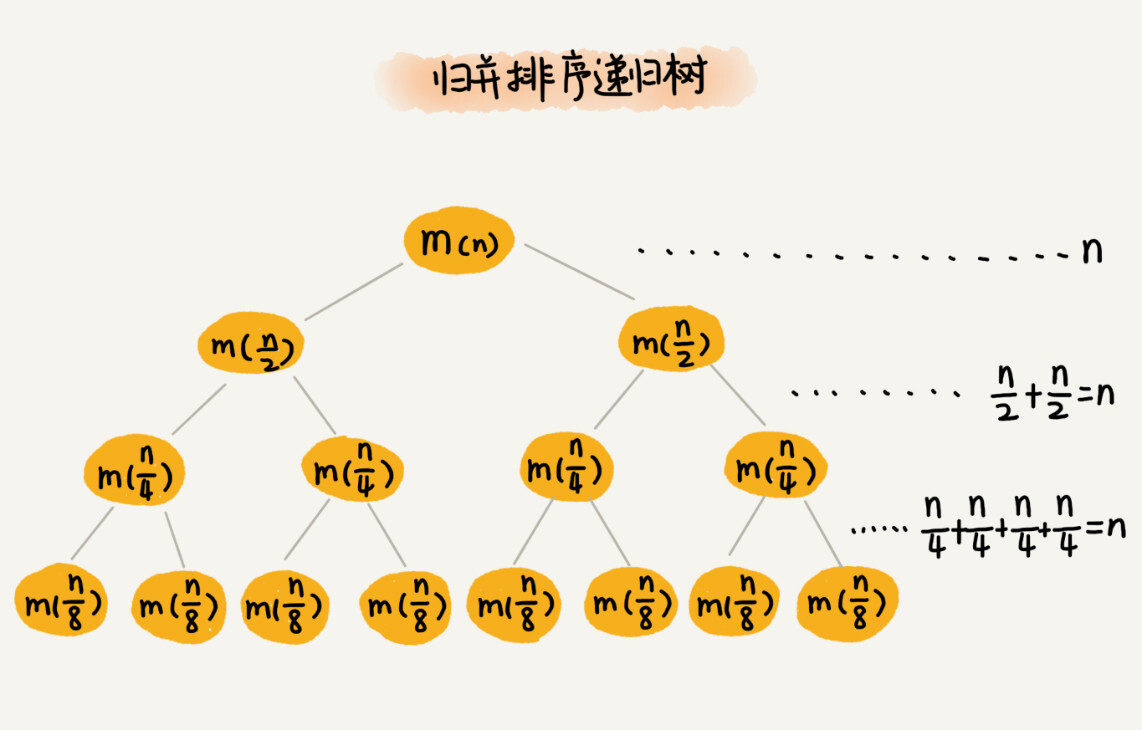
归并排序递归树是一颗满二叉树，满二叉树的高度大约是 log₂n，每一层的时间消耗为 n，所以归并排序实现的时间复杂度为 O(nlogn)。

 

关注微信公众账号「曹当家的」，订阅最新文章推送