8. 算法篇：递归

一、什么是递归？

1.递归是一种非常高效、简洁的编码技巧，一种应用非常广泛的算法，比如 DFS 深度优先搜索、前中后序二叉树遍历等都是使用递归。

2.方法或函数调用自身的方式称为递归调用，调用称为递，返回称为归。

3.基本上，所有的递归问题都可以用递推公式来表示，比如

f(n) = f(n-1) + 1，其中f(1)=1  
f(n) = f(n-1) + f(n-2)，其中f(1)=1, f(2)=2;  
f(n) = n*f(n-1)，其中f(1)=1;  

二、为什么使用递归？递归的优缺点？

1.优点：代码的表达力很强，写起来简洁。

2.缺点：空间复杂度高、有堆栈溢出风险、存在重复计算、过多的函数调用会耗时较多等问题。

三、什么样的问题可以用递归解决呢？

一个问题只要同时满足以下3个条件，就可以用递归来解决：

1.问题的解可以分解为几个子问题的解。何为子问题？就是数据规模更小的问题。

2.问题与子问题，除了数据规模不同，求解思路完全一样

3.存在递归终止条件

四、如何实现递归？

1.递归代码编写

写递归代码的关键就是找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，然后再推敲终止条件，最后将递推公式和终止条件翻译成代码。

2.递归代码理解

对于递归代码，若试图想清楚整个递和归的过程，实际上是进入了一个思维误区。

那该如何理解递归代码呢？如果一个问题A可以分解为若干个子问题B、C、D，你可以假设子问题B、C、D已经解决。而且，你只需要思考问题A与子问题B、C、D两层之间的关系即可，不需要一层层往下思考子问题与子子问题，子子问题与子子子问题之间的关系。屏蔽掉递归细节，这样子理解起来就简单多了。

因此，理解递归代码，就把它抽象成一个递推公式，不用想一层层的调用关系，不要试图用人脑去分解递归的每个步骤。

3.递归代码实现举例

案例一：想知道自己是在队伍中的第几排？

只能一排一排传递问前面的人，直到问到第一排的人再返回。 终止条件是 f(1)=1，公式 f(n) = f(n-1) + 1

def f(n):
    if n == 1:
        return 1
        
    return f(n-1) + 1

案例二：假如有 n 个台阶，每次你可以跨 1 个台阶或 2 个台阶，请问走这 n 个台阶有多少种走法？

可以根据第一步的走法分为两类，第一类是第一步走了 1 个台阶，那么剩下 n-1 个台阶的走法，第二类是第一步走了 2个台阶，那么剩下 n-2 个台阶的走法。
考虑终止条件：最后只可能剩下 1 或者 2 个台阶，分别走 1 和 2 种走法。

转化成公式：f(n) = f(n-1) + f(n-2), f(1)=1, f(2)=2。

def f(n):
    if n == 1:
        return 1
    if n == 2:
        return 2
        
    return f(n-1) + f(n-2)

案例三：App 做活动，假如 A 推荐 B 注册，B 推荐 C 注册…如何找到最终推荐人 A？

伪代码：

def findRootReferrerId(actorId) {
    referrerId = select referrer_id from [table] where actor_id = actorId
    if (referrerId == None)：
        return actorId;
    return findRootReferrerId(referrerId)

五、递归常见问题及解决方案

1.警惕堆栈溢出

可以声明一个全局变量来控制递归的深度，从而避免堆栈溢出。

如案例一，如果调用 f(10000) 就会报 RecursionError: maximum recursion depth exceeded in comparison，可以设置一个变量来控制递归深度：

depth = 0

def f(n):
	global depth
	depth += 1
	if depth > 500:
		raise RuntimeError('超出递归深度了')
	if n == 1:
		return 1

	return f(n-1) + 1

f = f(501)  # 将会抛出异常 RuntimeError('超出递归深度了')
print('f(n):', f)
print('depth:', depth)

2.警惕重复计算

通过某种数据结构来保存已经求解过的值，从而避免重复计算。

如：f(n) = f(n-1) + f(n-2) 这个例子，许多函数值都被重复计算了多次：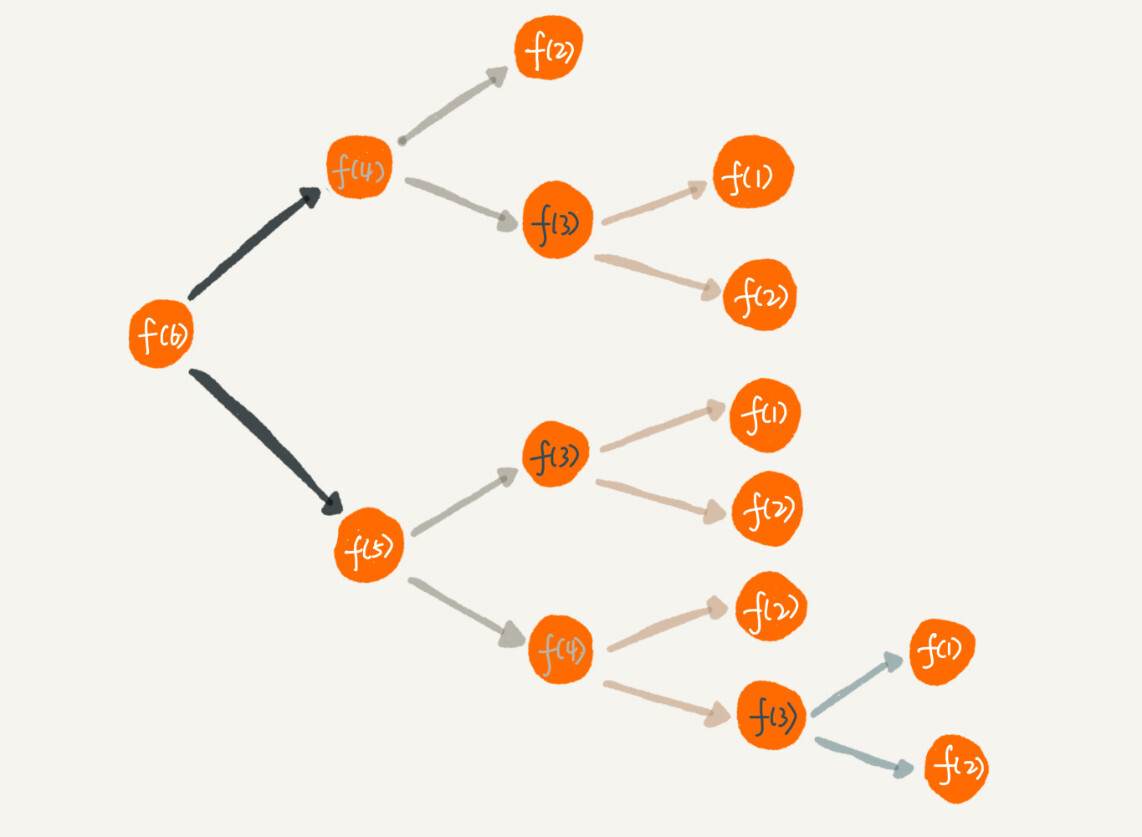

为了解决这个问题，可以通过一个数据结构（如 hashmap ）来保存已经求解过的 f(k)，当调用 f(k) 时，看是否已经求解过，如果 hashmap 中已经存在，则直接取值返回，不需要重复计算。

hashmap = {}
def f(n):
    if n == 1:
        return 1
    if n == 2:
        return 2
    
    if n in hashmap:
        print('f({})重复计算了'.format(n))
        return hashmap[n]
    ret = f(n-1) + f(n-2)
    hashmap[n] = ret
    return ret

f1 = f(6)
print(f1)

打印结果

f(3)重复计算了
f(4)重复计算了
13

六、如何将递归改写为非递归代码？

笼统的讲，所有的递归代码都可以改写为迭代循环的非递归写法。如何做？抽象出递推公式、初始值和边界条件，然后用迭代循环实现。

如：f(n) = f(n-1) + 1，f(1) = 1，改成：

def f(n):
    fn = 1
    for i in range(2, n+1):
        fn = fn + 1

    return fn

f(n) = f(n-1) + f(n-2), f(1) = 1, f(2) = 2，改成：

def f(n):
    if n == 1:
        return 1
    if n == 2:
        return 2

    ret = 0
    pre = 2
    prepre = 1
    for i in range(3, n+1):
        ret = pre + prepre
        prepre = pre
        pre = ret

    return ret

本文首发于 turbobin’s Blog 。转载请注明出处，附上本原文链接， 谢谢合作。

 

关注微信公众账号「曹当家的」，订阅最新文章推送