1. 衡量算法代码执行效率的指标：时间、空间复杂度

前言

最近在学习极客时间 王争 老师的《数据结构与算法之美》，以下是学习中的笔记，专栏中的一些伪代码、C 和 Java 语言的代码，基本用 Python 实现了一遍。

如涉及侵权问题，请联系我删除。

一、什么是复杂度分析？

1. 数据结构和算法解决是“快”和“省”的问题，即 “如何让代码运行更快、如何让代码更省空间”。因此需从执行时间和占用空间两个维度来评估数据结构和算法的性能。

2. 衡量算法执行效率的标准：时间复杂度和空间复杂度，二者统称为复杂度。
   时间复杂度：也叫渐进时间复杂度，表示的是算法的执行时间与数据规模增长之间的关系。 什么意思呢？假设你写了一段 for 循环代码，数据量有多大，里面的代码就会执行多少次，假设代码执行一次需要一个单位时间，那么，代码的执行时间就与数据量大小成正比 (这时候是线性关系)，但如果，for 循环的执行代码里面又加上了一个同样的 for 循环，即嵌套循环，那么执行时间对于同样的数据量就会成指数增长。时间复杂符表示的就是代码的执行时间与数据量之间是线性增长还是指数增长的关系。
   空间复杂度：类比时间复杂度，空间复杂度表示的是算法的存储空间和效率与数据规模增长之间的关系。 比时间复杂度分析容易很多，常见的空间复杂度就是 O(1)、O(n)、O(n^2)，其他的基本用不到。关于大 O 表示法请往下看。

二、为什么要进行复杂度分析？

1. 一般的性能测试确实可以测出代码的执行效率，但是一般代码的运行依赖操作系统环境等因素。和性能测试相比，复杂度分析有不依赖执行环境、成本低、效率高、易操作、提供理论性指导的特点。

2. 掌握复杂度分析，能编写出性能更优的代码，有利于降低系统开发和维护成本。

三、如何进行复杂度分析？

1. 大O表示法

1）来源
算法的执行时间与每行代码的执行次数成正比，这句话好理解，假设执行一次需要一个单位时间，执行次数越多自然执行时间就更高，我们用 T(n) = O(f(n)) 表示，其中 T(n) 表示算法执行总时间，f(n) 表示每行代码执行总次数，而 n 往往表示数据的规模。

2）特点

以时间复杂度为例，如这个公式T(n) = O(2n+3)，由于时间复杂度描述的是算法执行时间与数据规模的增长变化趋势，所以常量阶、低阶以及系数实际上对这种增长趋势不产决定性影响，所以在做时间复杂度分析时忽略这些项。这是数学中的极限思想。

2.复杂度分析法则

1）单段代码看高频：比如关注代码中有循环逻辑的那段代码。

2）加法法则：总复杂度等于量级最大的那段代码的复杂度。比如一段代码中有单循环和多重循环，那么取多重循环的复杂度。抽象成公式就是：O(n) = O1(n) + O2(n) = max(O1(n), O2(n))

3）乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积。比如递归、多重循环等。如嵌套循环的内循环和外循环都循环了 n 次，那么复杂度就为 O(n^2)

4）多个规模求加法：两个参数控制两个循环的次数，那么这时就取二者复杂度相加。比如方法中有 两段独立的循环代码，分别循环 m 次和 n 次，这时候无法判断哪个数据规模更大，那么复杂度就为 O(m+n)

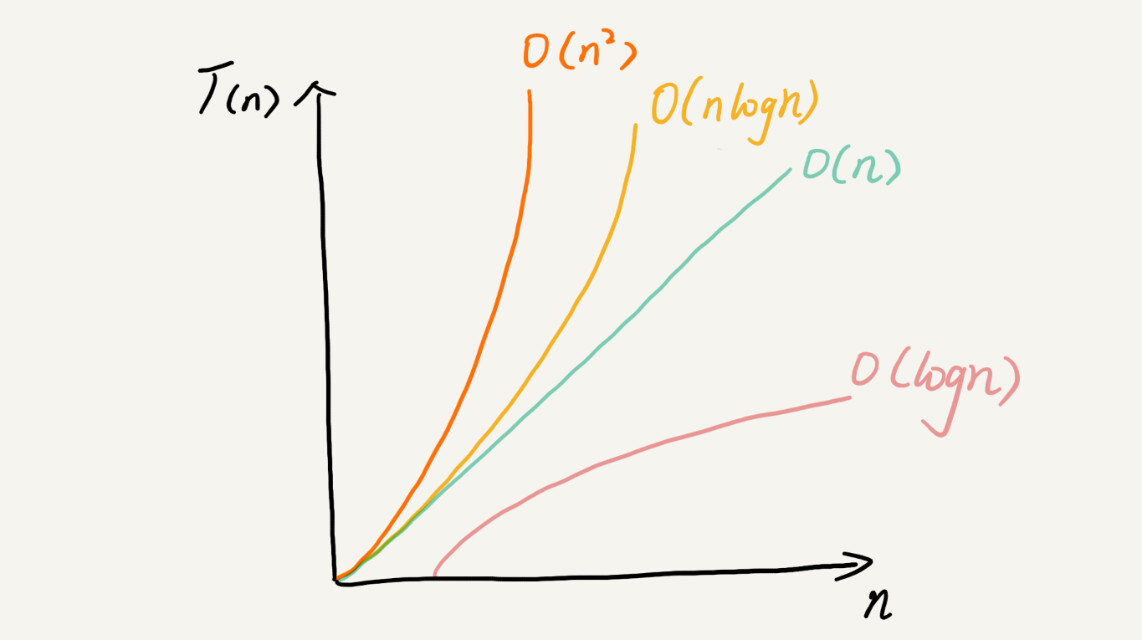
四、常用的复杂度级别

多项式阶

随着数据规模的增长，算法的执行时间和空间占用，按照多项式的比例增长。包括， O(1)（常数阶）、O(logn)（对数阶）、O(n)（线性阶）、O(nlogn)（线性对数阶）、O(n^2) （平方阶）、O(n^3) （立方阶）

1. O(1)

首先明确一点，它是一种常量数级的复杂度表示方法，并不是只执行了一行代码。只要代码的执行时间不随 n 的增大而增长，这样代码的时间复杂我们都记作 O(1)。 就算一段代码循环执行了 1000 次，10000 次，只要是确定的循环次数，它的复杂度也是O(1)。一般情况下，只要算法中不存在无法确定的循环语句、递归语句，即使有成千上行代码，其复杂度也是O(1)

2. O(logn)、O(nlogn)

对数阶时间复杂度。非常常见的一种时间复杂度，也是最难分析的一种，先看一段代码：

 i=1;
 while (i <= n)  {
   i = i * 2;
 }

这段代码每循环一次就乘以 2，当 i > n 时，循环结束。可以运用高中学过的等比数列的知识: 2^x = n，x 表示循环的次数，只要求出 x 的值，时间复杂度就可以表示出来了。很显然 x=log₂n，即时间复杂度为 O(log₂n)。

如果把上面代码 2 改成 3：

 i=1;
 while (i <= n)  {
   i = i * 3;
 }

同样的分析可以得出时间复杂度为 O(log₃n)。 而 log₃n = log₃2 * log₂n，利用乘法法则，可以得出 O(log₃n) = O(C * log₂n), C 是常量系数，在时间复杂度表示中可以忽略，因此：O(log₃n) = O(log₂n)。可以看出，对数的‘底数’可以忽略，因此可以统一表示成 O(logn)。

而 O(nlogn) 理解起来就很容易了，就是一段时间复杂度为 O(logn) 的代码循环了 n 遍。

3. O(n)、O(n²)…

这个比较容易了，就是一段代码循环 n 次，2 层嵌套循环 n 次，3 层嵌套循环 n 次…

4. 各个类型的时间复杂度对比

非多项式阶

随着数据规模的增长，算法的执行时间和空间占用暴增，这类算法性能极差。包括， O(2ⁿ)（指数阶）、O(n!)（阶乘阶）

关于 O(n!) 算法讲一个典型案例：旅行商的例子。
一位旅行商需要前往 5 个城市，同时要保证旅程最短，为此要考虑前往这些城市的顺序。

数学上就想象成 5 个不同的分散的点，从一个点出发，需要把 5 个点都连起来，计算每个点连接的直线距离之和。最后取路程最短的那种连法。

考虑到不同的连接先后顺序，5 个点有 5! = 120 种不同的排列组合。 推而广之，当涉及到 n 个城市时，就需要操作 n! 次才能得出结果。这种算法非常耗时。

五、如何掌握好复杂度分析方法？

复杂度分析关键在于多练，理解概念，适度刷题。

学习书单推荐：

入门趣味算法书

《大话数据结构》：有趣、不枯燥、400 多页，基本两三天能看完，看完后对算法有一个直观的感受。

《算法图解》：“像小说一样有趣的入门算法书”，通俗易懂，不到 200 页，内容较少，看完对数据结构和算法有个直观的认识。

入门书的共同问题是缺少细节，不够系统，也不够严谨。

针对特定编程语言的教科书

《数据结构与算法分析：C 语言描述》
《数据结构与算法分析：Java 语言描述》
《数据结构与算法分析：Python 语言描述》

教科书版。系统、严谨、全面。这是同一个作者用不同的语言写了三个版本的书籍。

面试必刷宝典

《剑指 Offer》：应付面试，很多经典、常见的面试题
《编程珠玑》：特色是讲了很多针对海量数据的处理技巧，值得一看。
《编程之美》：这本书有多位作者，大部分是微软的工程师，题目稍难，适合钻研。

经典

《算法导论》：经典，但是很厚，啃起来很费劲，充斥各种算法的正确性、复杂度的证明、数学公式推导。
《算法 第 4 版》：经典，豆瓣评分 9.4。相对友好很多，也容易看懂，书中算法使用 Java 语言。偏重讲算法，数据结构讲的不多，内容可能有些不够全面，比如没有涉及动态规划的内容。

殿堂级经典

《计算机程序设计艺术》：算法学习的终极挑战。
整套书无论是广度、深度、系统性、全面性都是其他书籍无法相比的，需要很好的数学、算法、计算机基础。

闲暇阅读

《算法帝国》：文科生都能看懂

《数学之美》：吴军老师的手笔

《算法之美》

本文首发于 turbobin’s Blog 。转载请注明出处，附上本原文链接， 谢谢合作。

 

关注微信公众账号「曹当家的」，订阅最新文章推送