11. 算法篇：线性排序

线性排序

有三种排序算法的时间复杂度为 O(n)，因此这类排序算法叫线性排序。这三种算法主要是：桶排序，计数排序，基数排序。这三个算法都是基于非比较的排序算法，且对应用场景比较苛刻。

桶排序(Bucket sort)

核心思想：将要排序的数据分到几个有序的桶里，每个桶里的数据再单独进行排序，桶内排完后再把数据按照顺序取出，组成的序列就是有序的了。

复杂度分析：

如果要排序的数据有 n 个，我们把它们均匀地划分到 m 个桶内，每个桶里就有 k=n/m 个元素。每个桶内部使用快速排序，时间复杂度为 O(k * logk)。m 个桶排序的时间复杂度就是 O(m * k * logk)，因为 k=n/m，所以整个桶排序的时间复杂度就是 O(n*log(n/m))。当桶的个数 m 接近数据个数 n 时，log(n/m) 就是一个非常小的常量，这个时候桶排序的时间复杂度接近 O(n)。

桶排序的适用范围

桶排序首先要知道数据的范围，能很容易的将数据划分到 m 个桶，其次，要求各个桶之间的分布是比较均匀的，数据经过桶的划分后能比较平均的把数据划分到各个桶内，不然，如果许多数据划分到一个桶内，桶排序就退化成快排了。

桶排序其实比较适合用到外部排序中，数据存储在磁盘上，数据量比较大，而机器内存有限，无法将数据全部加载到磁盘。

比如 10 Gb 数据的订单，按照订单金额排序，金额范围为 1 ~ 10万元。那么可以根据金额划分到 100 个桶内，第一个桶存储金额在 1~1000元的订单，第二个桶存储 1001~2000 的订单。每个桶对应一个文件，顺序命名。那么可以按顺序依次将每个文件加载到内存排序。

计数排序(Counting sort)

计数排序其实是桶排序的一种特殊情况，当要排序的 n 个数据，所处的范围不大，比如最大值为 k，那么可以将数据划分为 k 个桶，每个桶内的数据都是相同的，节省了桶内排序的时间。

比如对 50 万考生按照成绩排名，成绩满分为 900 分，最小是 0 分。那么可以将 50万划分到 901 个桶里，桶内的都是分数相同的考生，所以不需要排序，只需要依次扫描每个桶就实现了 50 万考生的排序，因为只涉及到遍历操作，所以时间复杂度为 O(n)。

计数排序只能用在数据范围不大的场景中，如果数据范围 k 比要排序的数据 n 大很多，就不适合用计数排序了。而且，计数排序只能给非负整数排序，如果要排序的数据是其他类型的，要将其在不改变相对大小的情况下，转化为非负整数。

计数排序的实现过程

假设 8 个考生，分数在0~5 分之间，每个考生分数依次是：A[8] = 2，5，3，0，2，3，0，3。

将数据划分到 6 个桶里（创建一个长度为 6 的数组 C[6]），下标 0~5 对应分数，每个桶存放分数对应的考生个数：C[6] = 2，0，2，3，0，1

改造数组 C[6]，对数组顺序求和，每个数组元素存储顺序累加的值：C[6] = 2，2，4，7，7，8

对数组 A[8] 从后往前扫描，当扫描到分数 3 时，从数组 C[6] 的下标 3 中取出元素 7，说明分数小于等于 3 的考生有 7 个，于是将 3 放到临时数组 R 的第 7 的位置（下标 6），同时，C[3] 对应的值减 1，变成 6。依次类推。

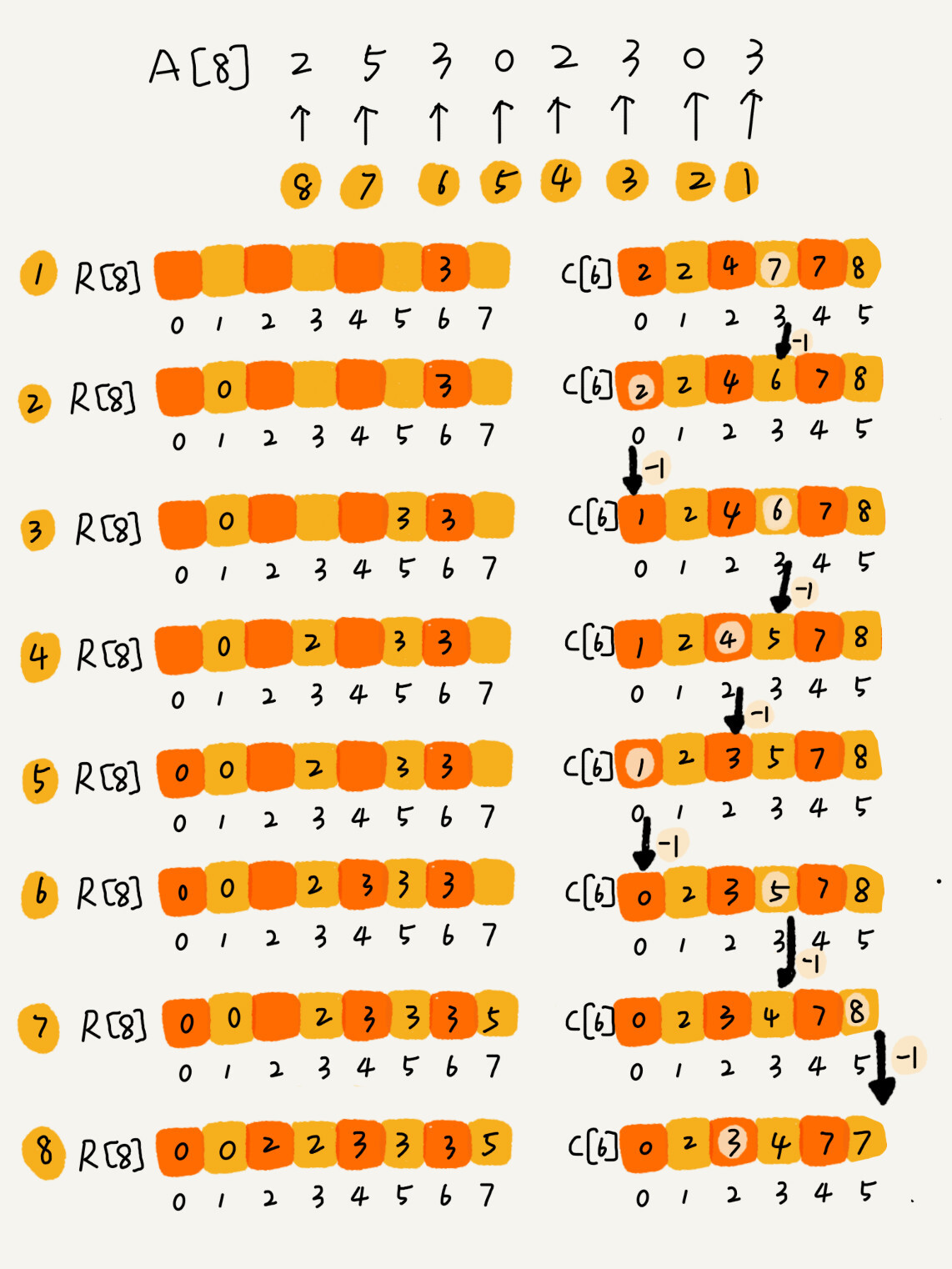
实现代码如下：

# -*- coding: utf-8 -*-

"""
计数排序
"""

def count_sort(arr):
    n = len(arr)
    if n <= 1:
        return arr
    # 获取数组的范围
    max_num = max(arr)
    # 申请一个大小为 max_num 的初始化数组
    C = [0] * (max_num + 1)
    # 计算每个元素的个数
    for i in arr:
        C[i] += 1
    # 依次累加
    for j in range(1, max_num+1):
        C[j] = C[j-1] + C[j]
    # 临时数组 R，存储排序后的结果
    R = [None] * n
    for k in arr[::-1]:
        index = C[k] - 1
        R[index] = k
        C[k] -= 1
    return R


if __name__ == '__main__':
    arr = [2, 5, 3, 0, 2, 3, 0, 3]
    print(count_sort(arr))

基数排序(Radix sort)

问题：如何在 O(n) 时间复杂度内给 10 万个手机号码从小到大排序？

桶排序，计数排序要求数据有一定的范围，而手机号码有 11 位，范围太大，要做到在 O(n) 时间范围内排序，可以使用基数排序。

核心思想

要排序的数据有个特点，如果 a 号码的前几位比 b 号码的前几位大，那么 a 号码就比 b 号码大，后面的位就不用比较了。我们可以先从最后一位来排序，然后按照倒数第二位重新排序，以此类推，最后按照第一位来排序，拍完后，手机号码就有序了。

例如：给数据 [269，157，348] 排序，排序过程为 [157, 348, 269] -> [348, 157, 269] -> [157, 267, 348]

时间复杂度

每一位的排序，因为数字范围是 0~9，因此可以使用计数排序，时间复杂度为 O(n)，手机号码有 11 位，要经过 11 次的计数排序，时间复杂度为 O(k * n)，k=11，所以基数的排序近似于 O(n)。

扩展

手机号码是固定的等长的 11 位，如果不是等长的数据，那么位数不够的，可以暂时在后面补 0，因为根据 ASCII 值，所有的字母，数字都大于 0，所以比较中不会影响到原有数据的大小。

小结

基数排序对要排序的数据是有要求的，需要可以分割出独立的“位”来比较，而且位之间有递进的关系，如果 a 数据的高位比 b 数据大，那剩下的低位就不用比较了。除此之外，每一位的数据范围不能太大，要可以用线性排序算法来排序，否则，基数排序的时间复杂度就无法做到 O(n) 了。

排序算法总结

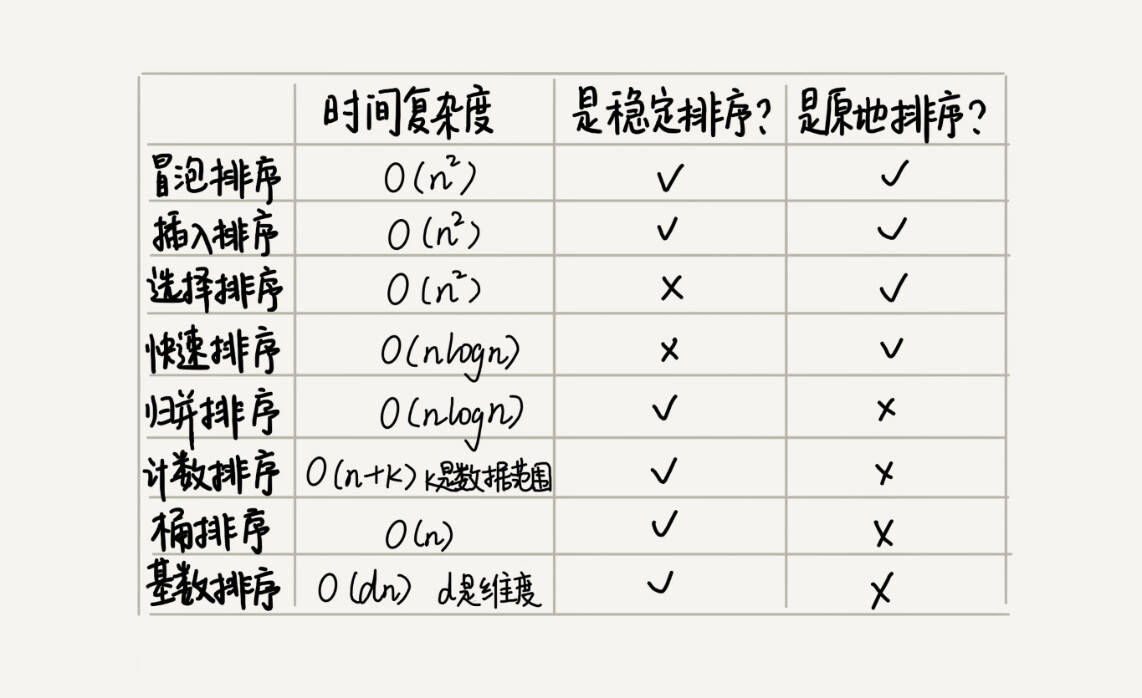
比较上面几种排序，如果要一个通用且高效的排序算法，通常会选择时间复杂度为 O(nlogn) 的排序算法，也就是归并排序和快速排序。对于数据量小且内存充足的情况下，一般使用归并排序，时间复杂度比较稳定，而快速排序有可能退化到 O(n^2)。

对于数据量内存占用较大的数据，一般使用快速排序，这时候为了避免时间复杂度退化，需要选择合适的分区点，而不能每次单纯取区间的最后一位。为了让分区的数据比较平均，分区点的选取一般有两种方法：

• 三数取中法：从区间的首、尾、中取出一个数，对比大小，取 3 个数的中间值作为分区点。但是，如果数组区间较大，可能要“五数取中”或“十数取中”了
• 随机法：从区间中随机选取一点作为分区点。

 

关注微信公众账号「曹当家的」，订阅最新文章推送