3. 数据结构篇:数组
数组在很多编程语言中都是基本的数据类型,使用非常广泛和普遍,同时它也是最基本的一种数据结构。虽然很多人能熟练使用它,但是仍然有许多人不清楚它的结构和特点。
什么是数组? 专业的定义是:数组是一种线性表数据结构,它用一组连续的内存空间来存储一组具有相同类型的数据。
1.线性表
顾名思义,线性表就是数据排成一条线一样的结构。除了数组,链表、栈、队列也是一种线性表结构。 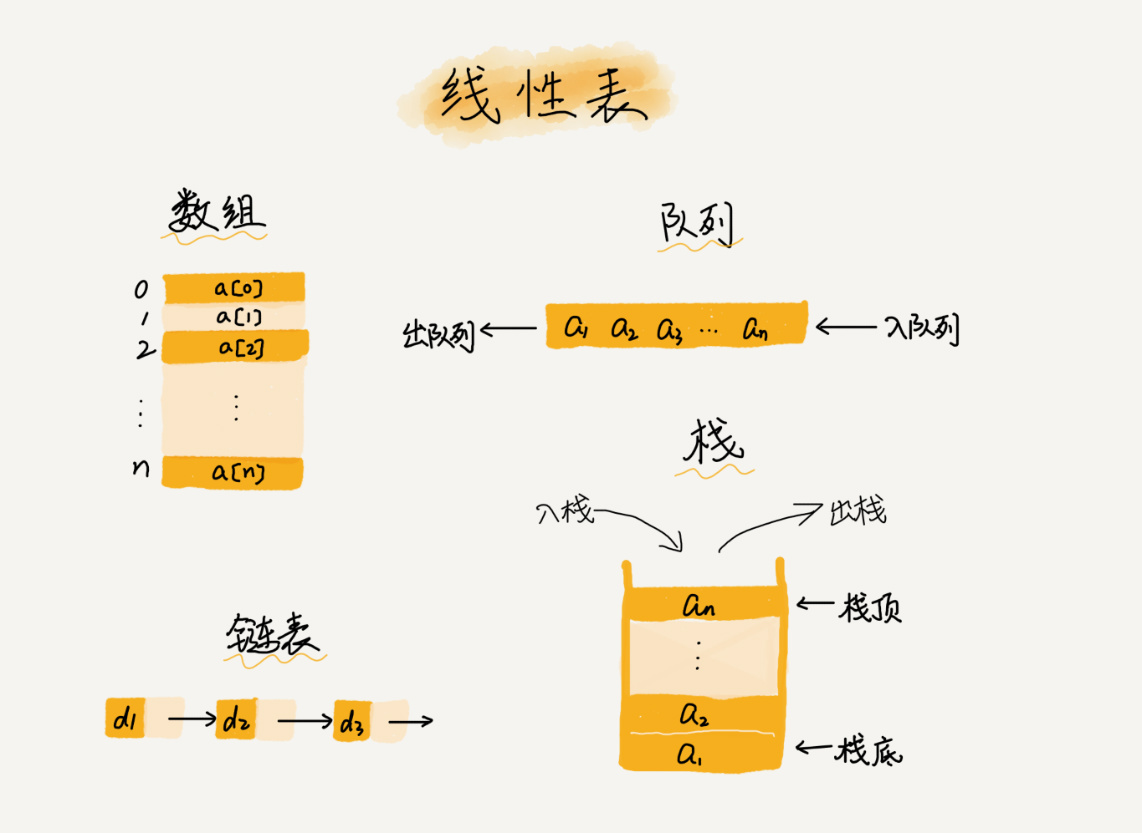
与其对应的就是非线性表结构,如二叉树、堆、图等。 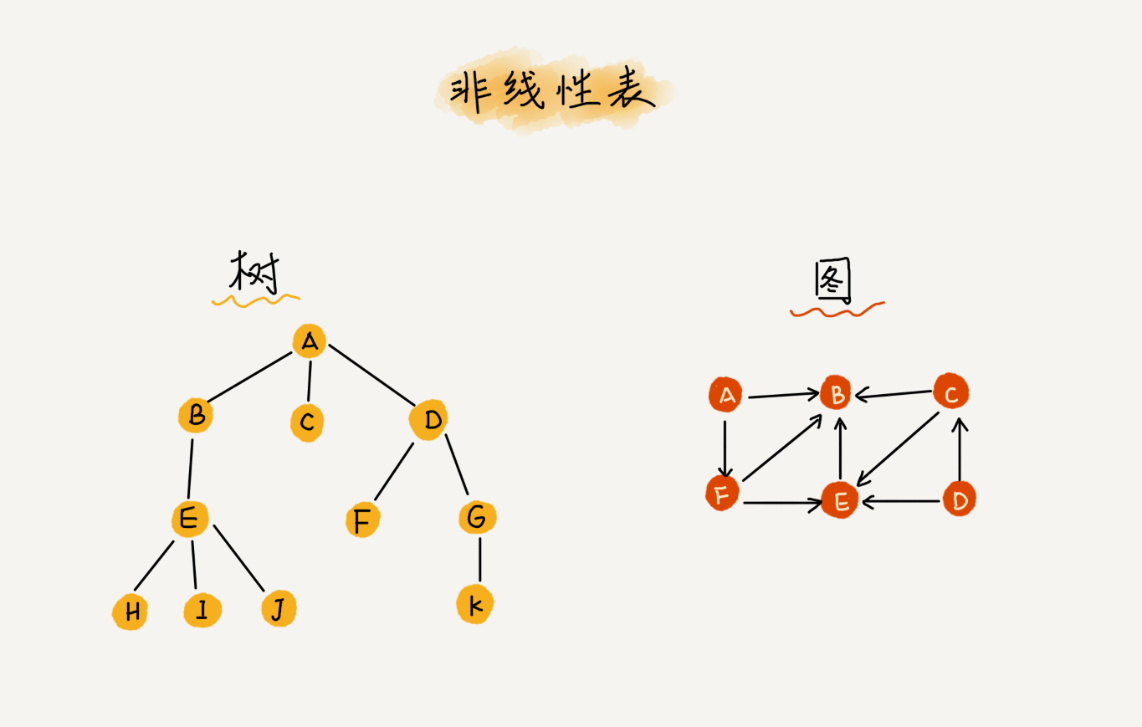
2.连续的内存空间和相同类型的数据
创建一个数组,需要在内存中开辟一块连续的内存空间,并且对数组的所有操作都必须保证内存的连续性。可以想象成数组就是计算机内存中一组排在一起的箱子,箱子上面有连续的编号(从 0 开始),箱子之间不能有空位置。
这个特性使得数组可以实现根据下标对元素进行随机访问,且速度非常快,时间复杂度为 O(1)。但是也有一个缺点,就是插入和删除元素的操作变得很慢,因为插入或者删除之后为了保证内存的连续性,要进行大量的数据搬移。
数组如何根据下标对元素进行随机访问呢?它有一个寻址公式,可以快速定位任何元素的地址:
a[i]_address = base_address + i * data_type_size
它表示,第 i 个元素的地址 = 基地址/首地址(即下标为 0 元素的地址) + 元素下标 * 元素类型的大小
比如存储 int 类型的元素,首地址为 1000,1 个 int 占 4 个字节,那么 第 i 个元素的地址就很容易计算出来。 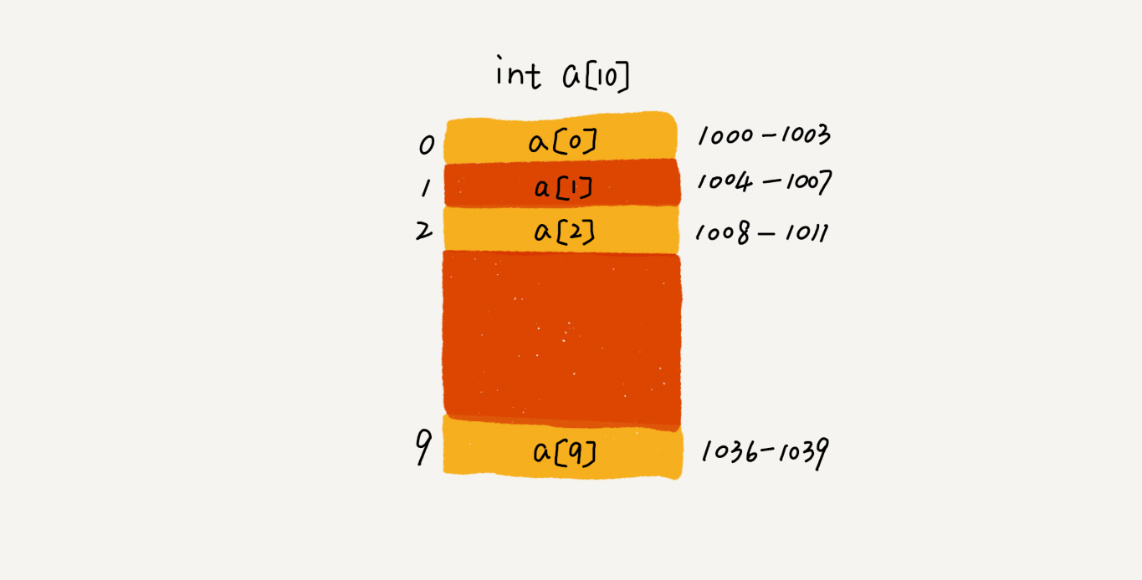
拓展
为什么数组的插入和删除操作会很低效?有什么改进的思想?
先来看插入操作
假设数组的长度为 n,如果要在第 k 的位置插入一个元素,为了腾出位置,第 n 到 n-k 位置的数据都需要往后挪动一位。
分析这种情况的复杂度,如果是在数组末尾插入元素,就不需要进行数据的搬移,这是最好情况时间复杂度,为 O(1),如果在数组头部(下标 0 的位置)插入,就得出最坏情况时间复杂度为 O(n),因为在每个位置插入的概率是相同的,所以平均时间复杂度就为 (1+2+3+…+n)/n = O(n)。
有什么办法可以避免大规模数据搬移呢?分两种情况:
- 数组中元素是有序的,那么就必须按照上面的情况进行数据搬移。
- 如果数组是无序的,当在第 k 个位置插入元素时,可以先把原来第 k 个元素挪到数组的末尾,再将新的元素插入到 k 的位置,这时候就不需要进行大规模数据搬移,时间复杂度降为 O(1)。这是快排中会用到的思想。
再来看删除操作
如果要在第 k 个位置删除一个元素,和插入一样,为了内存的连续性,需要将 n-k 到 n 的元素往前挪一位。最好情况时间复杂度为 O(1),最坏情况时间复杂度为 O(n),平均时间复杂度也为 O(n)。
这里为了避免大规模的数据搬移也可以想办法改进:
我们每次执行的删除操作并不用真正的删除数据,而是先打上一个”标记”,等到标记比较多,元素连续的时候,再执行一次真正的删除操作。这种做法就大大减少了频繁的数据搬移。 
其实,这也是 GC(垃圾回收) 中 标记-清除 的核心思想。
再次拓展
Python 中垃圾回收机制主要有三种:引用计数、标记-清除、分代回收。
以引用计数为主,以 标记-清除、分代回收为辅。
引用计数:指一个对象被引用 1 次,计数就+1,当引用减少,次数变为 0 时,该对象的生命周期就结束了。
标记清除:当内存中的对象被删除时,会先打上删除标记,在内存中就访问不到了,当没有空闲内存的时候,会遍历内存中所有的对象,把能访问到的打上正常标记,然后清扫一遍内存,把没有标记的对象或有删除标记的对象释放。
分代回收:把系统中的所有内存按其存活时间划分为不同的集合,每个集合称为一个‘代’。比如当内存块 M 经过三次垃圾回收之后还存活,就把它划分到集合 A 中,而把新分配的内存分配到集合 B 中,大多数情况下只对集合 B 做垃圾回收,而集合 A 中轮询的时间间隔比较长一点,在这个过程中,集合 B 中存活时间长的对象会被转移到集合 A 中。
本文首发于 turbobin’s Blog 。转载请注明出处,附上本原文链接, 谢谢合作。

关注微信公众账号「曹当家的」,订阅最新文章推送