16. 数据结构篇:二叉树
树 (Tree)
树是一种非线性的表结构。
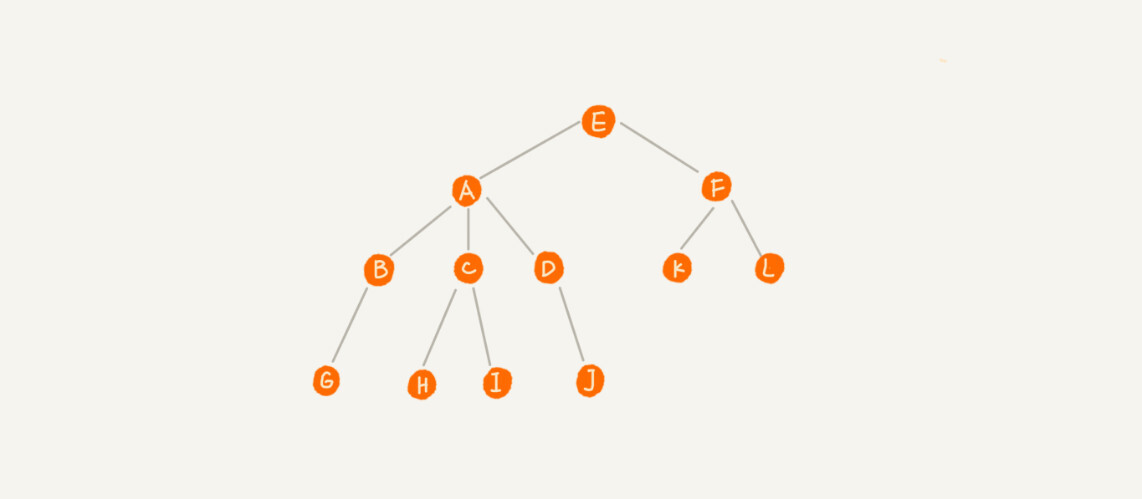
A 节点就是 B 节点的父节点,B 节点是 A 节点的子节点。B、C、D 这三个节点的父节点是同一个节点,所以它们之间互称为兄弟节点。我们把没有父节点的节点叫做根节点,也就是图中的节点 E。我们把没有子节点的节点叫做叶子节点或者叶节点,比如图中的 G、H、I、J、K、L 都是叶子节点。
此外,还有树的高度、深度、层数等概念。
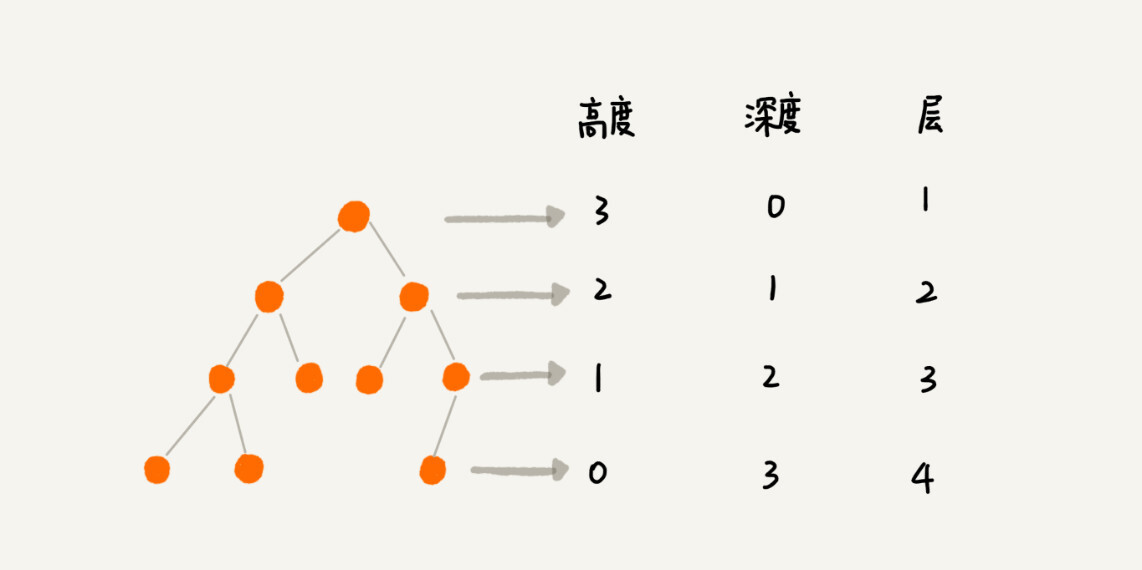
二叉树
二叉树,也就是每个节点最多只有两个节点,分别是左子节点和右子节点。
二叉树根据形状,有两个比较特殊的二叉树,分别是满二叉树和完全二叉树。
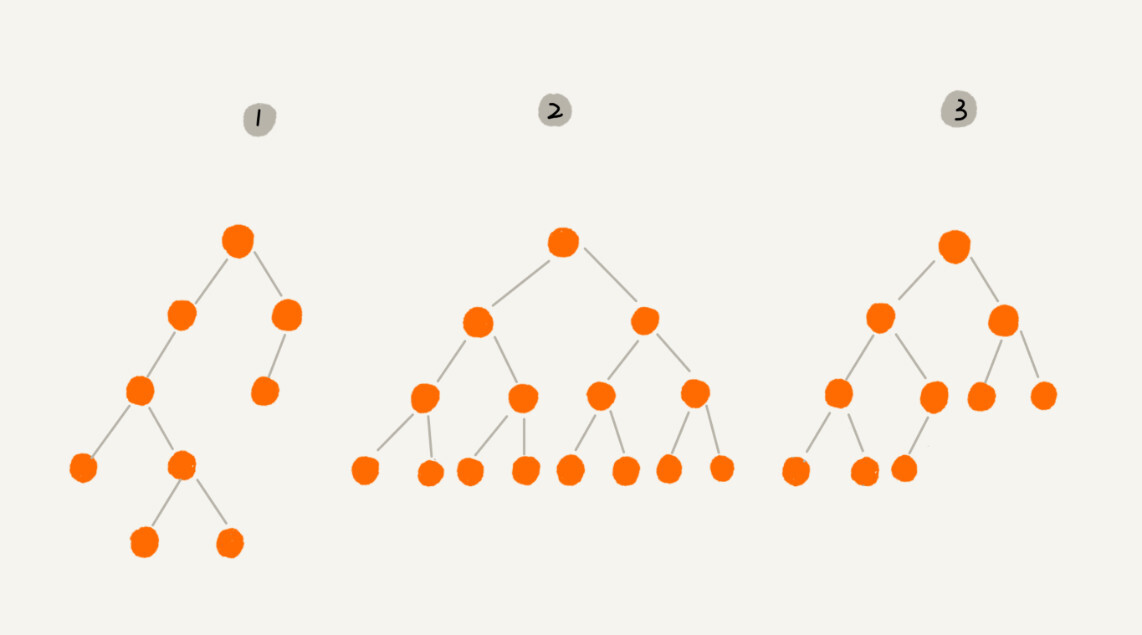
编号 2 中,叶子节点全都在最底层,除了叶子节点外,每个节点都有左右两个子节点,这种就叫做 满二叉树。
编号 3 中,叶子节点都在最底下两层,最后一层的叶子节点都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大,这种就叫做完全二叉树。
二叉树的存储
链式存储法
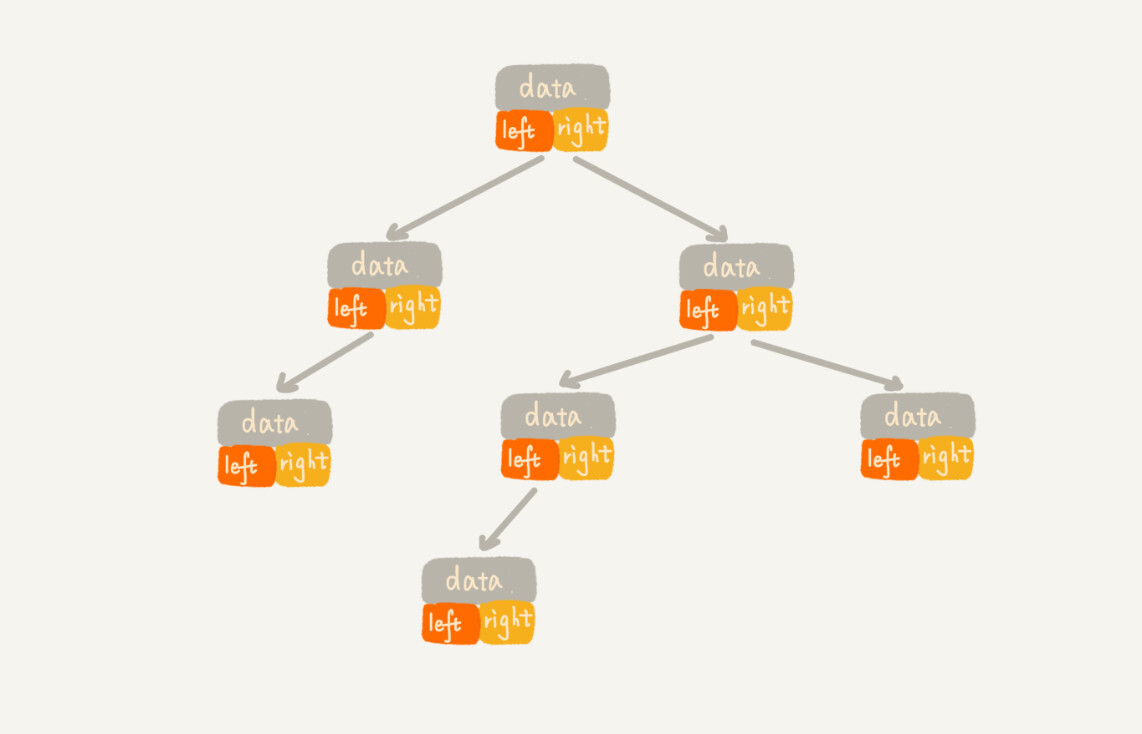
每个节点有三个字段,其中一个存储数据,另外两个是指向左右子节点的指针。因此,只要知道根节点,就可以通过左右指针把整棵树串起来。
顺序存储法
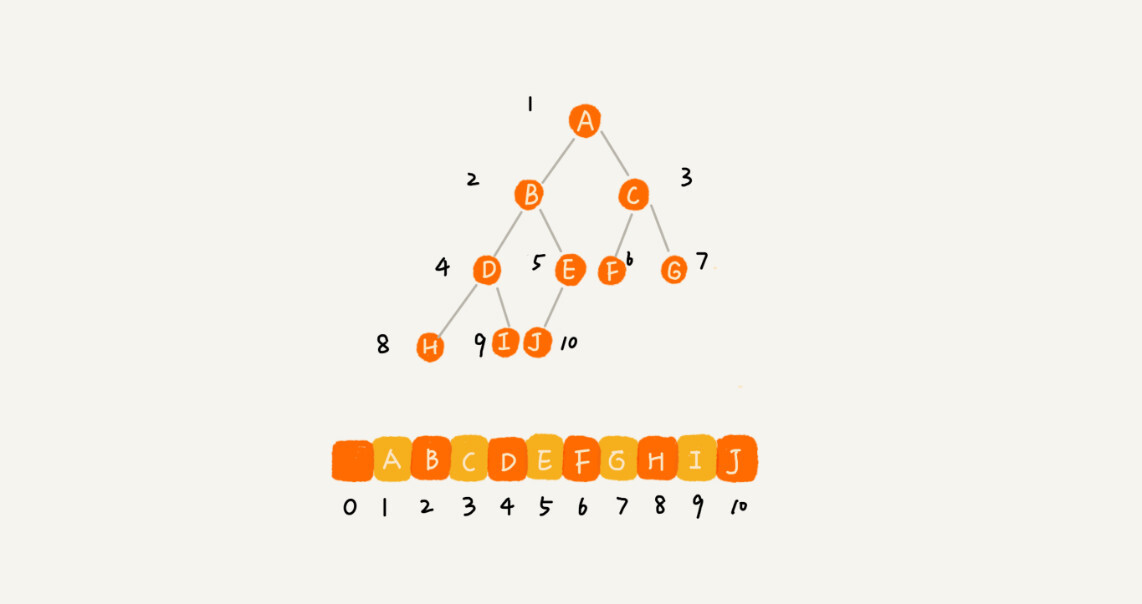
把跟节点存储在下标 i = 1 的位置,那左子节点存储在下标 2 * i = 2 的位置,右子节点存储在 2 * i + 1 = 3 的位置。以此类推,B 节点的左子节点存储在 2 * i = 2 * 2 = 4 的位置,右子节点存储在 2 * i + 1 = 2 * 2 + 1 = 5 的位置。
完全二叉树使用数组的存储是最省内存的方式,只空出了下标为 0 的位置(这样做是为了方便计算),而非完全二叉树如果使用数组存储就会浪费比较多的内存。
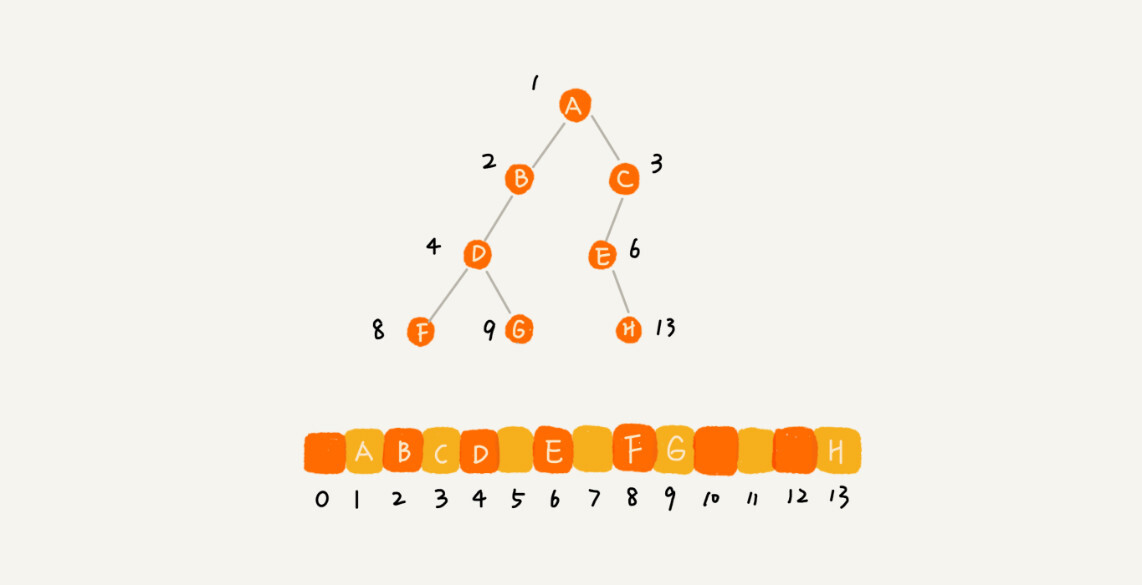
二叉树的遍历
二叉树的遍历通常有三种方法:前序遍历、中序遍历、后序遍历。这里的前中后表示的是它的左右子树节点遍历打印的先后顺序。
- 前序遍历是指,对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树。
- 中序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它本身,最后打印它的右子树。
- 后序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个节点本身。
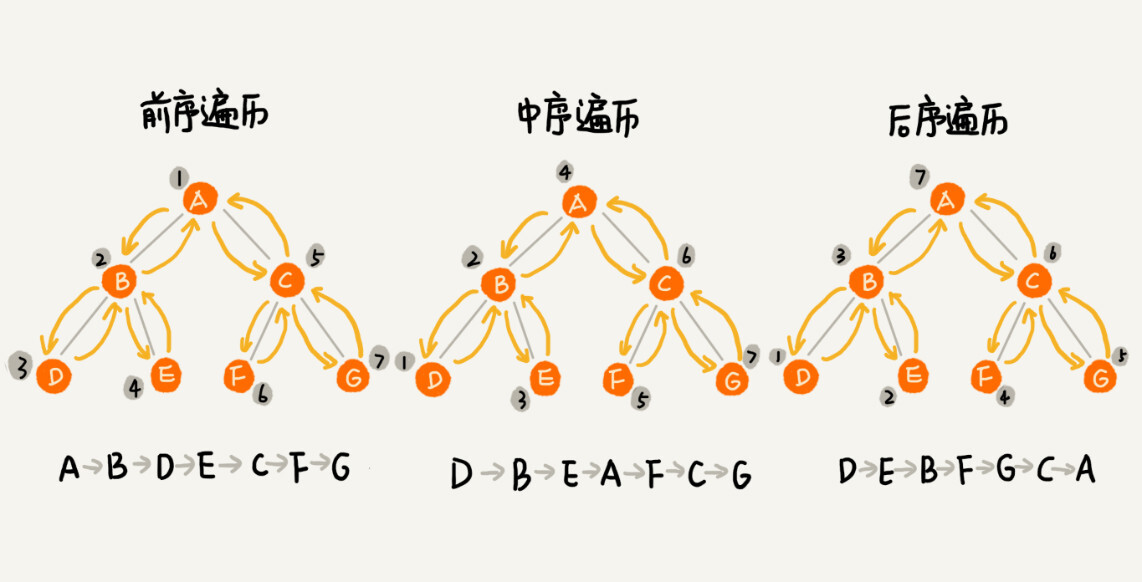
实际上,二叉树的前、中、后序遍历就是一个递归的过程。
void preOrder(Node* root) {
if (root == null) return;
print root // 此处为伪代码,表示打印root节点
preOrder(root->left);
preOrder(root->right);
}
void inOrder(Node* root) {
if (root == null) return;
inOrder(root->left);
print root // 此处为伪代码,表示打印root节点
inOrder(root->right);
}
void postOrder(Node* root) {
if (root == null) return;
postOrder(root->left);
postOrder(root->right);
print root // 此处为伪代码,表示打印root节点
}
二叉查找树
二叉查找树也叫二叉搜索树,可以实现快速的查找、插入、删除一个数据。
二叉查找树要求:每个节点的左子树中的每个节点的值都要小于这个节点的值,而右子树节点的值都要大于这个节点的值。
1. 二叉树的查找操作
思路:从根节点开始查找,如果值等于根节点,那就直接返回。如果小于根节点的值,那就在左左子树中递归查找;如果大于根节点的值,那就在右子树中递归查找。
实现代码如下:
# -*- coding: utf-8 -*-
class TreeNode:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
class BinarySearchTree:
def __init__(self, data=[None]):
self.root = TreeNode(data[0])
def find(self, data):
p = TreeNode(self.root)
while p != None:
if data < p.data:
p = p.left
elif data > p.data:
p = p.right
else:
return p
return None
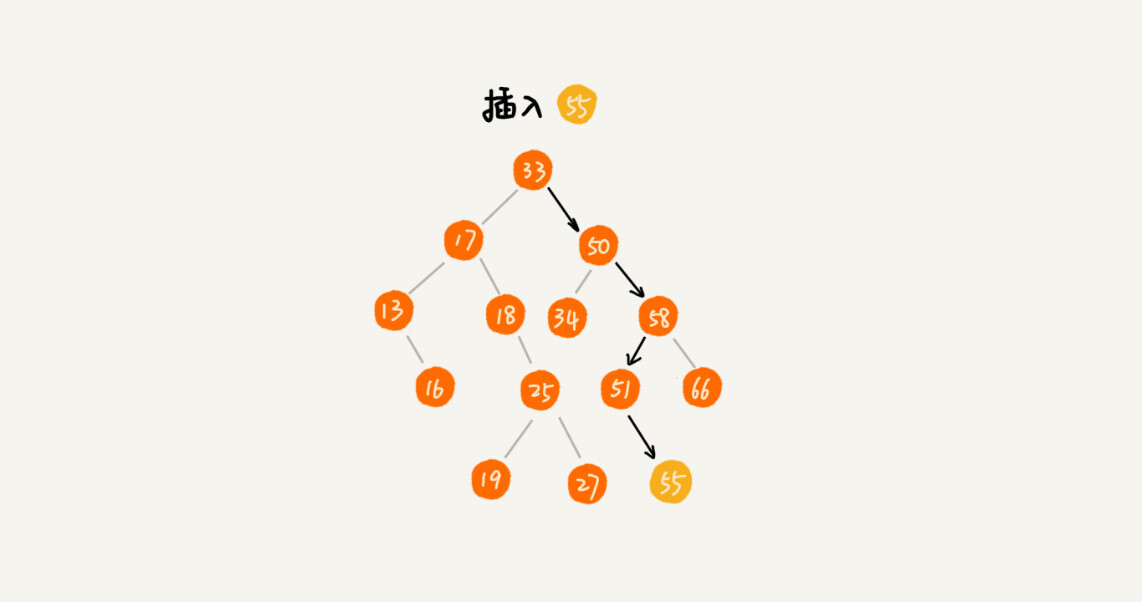
2. 二叉查找树的插入操作
插入操作跟查找类似,从根节点开始,依次比较要插入的数据和节点的大小关系,
3. 二叉查找树的删除操作
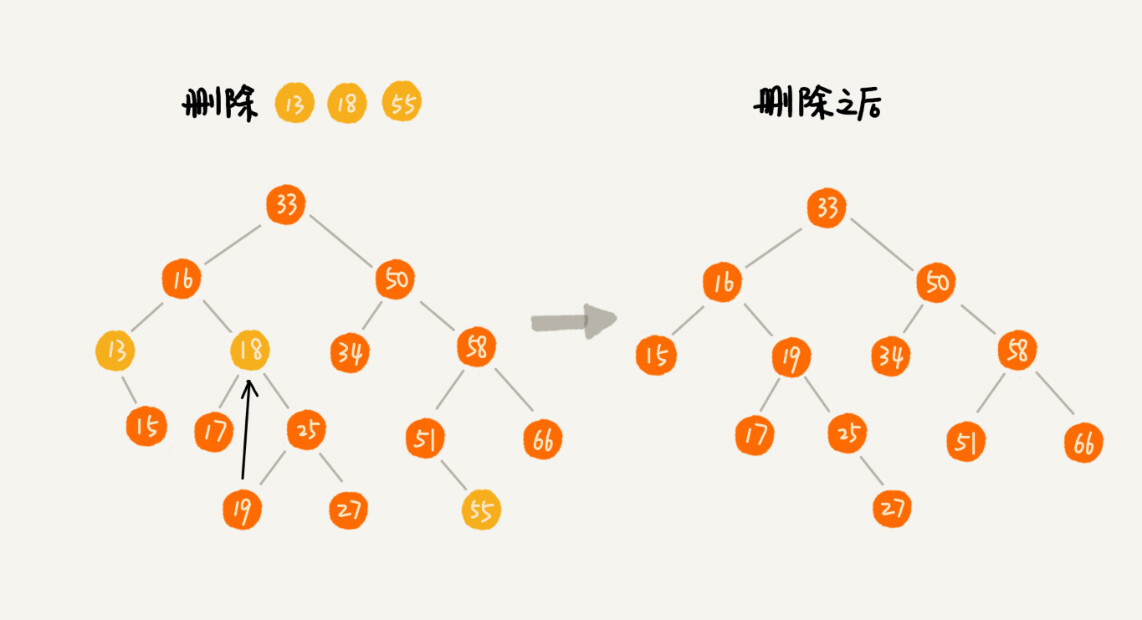
删除操作比较复杂,可以分为三种情况:
- 如果要删除的节点没有子节点,那么只需要将它的父节点指向 null
- 如果要删除的节点只有一个节点(只有左子节点或右子节点),那么只需要更新它的父节点的指针指向它的子节点
- 如果要删除的节点有两个子节点,就有点复杂了。首先要找到这个节点的右子树的最小节点,把它替换到要删除的节点上。然后再删除掉这个最小节点(最小节点肯定没有左子节点),
实际上,二叉树的删除操作有个简化的方法,就是单纯地把将要删除的节点标记为“已删除”,而并不是把这个节点从树中去掉。
4. 二叉查找树的其他操作
除了插入、删除、查找操作外,二叉查找树还支持快速地查找最大和最小节点,前驱节点和后继节点。
二叉查找树的中序遍历可以输出有序的数据序列,时间复杂度为 O(n)。因此,二叉查找树叶叫做二叉排序树。
二叉查找树的时间复杂度分析
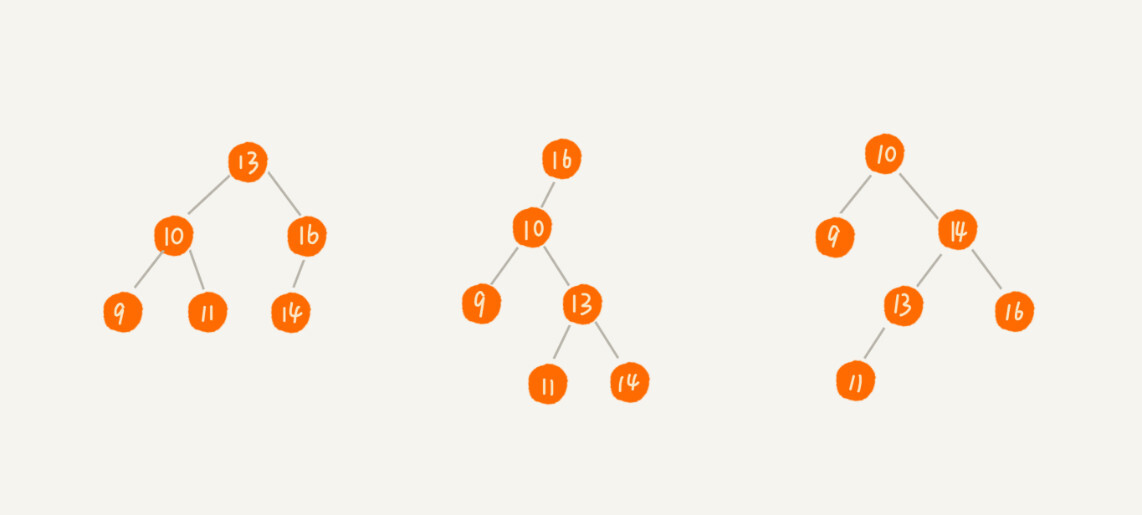
二叉查找树的插入、删除、查找操作的时间复杂度跟二叉树的形态有关,准确的说,是与树的高度成正比。
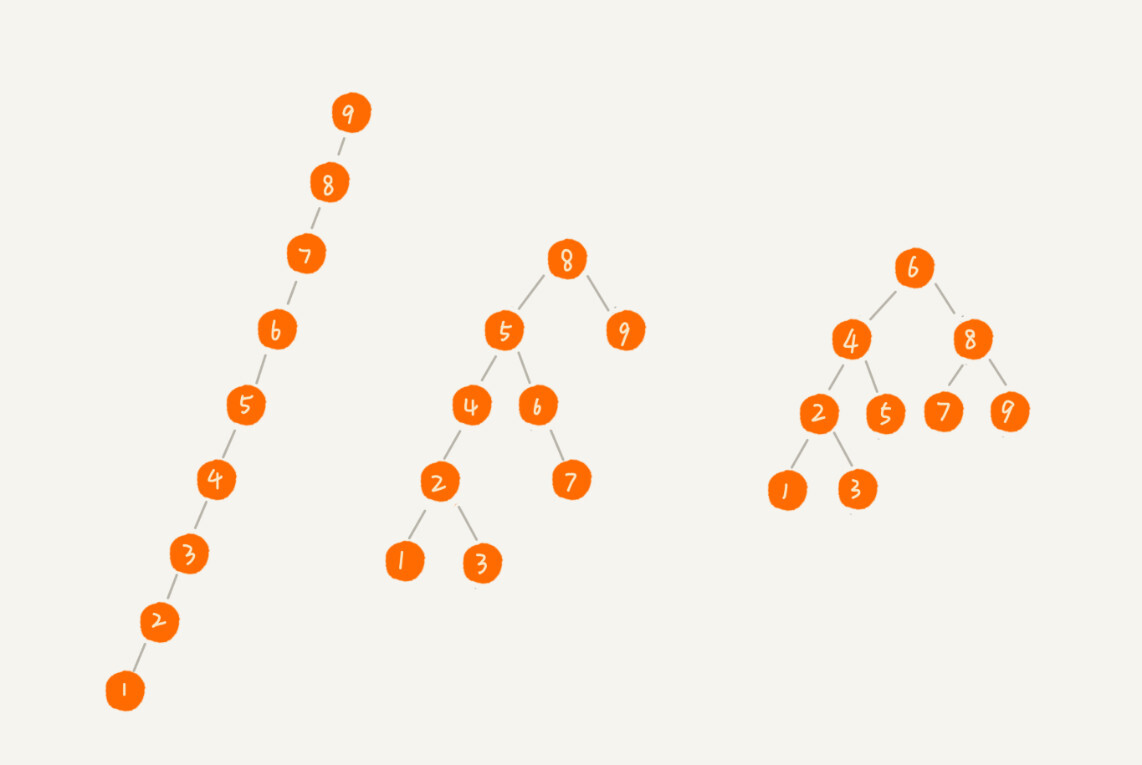
第一种二叉树已经极度不平衡,退化成了链表,树的高度就是节点的个数,时间复杂度为 O(n)。
第三种完全二叉树,它的高度小于等于 log2n,因此时间复杂度为 O(logn)。

关注微信公众账号「曹当家的」,订阅最新文章推送