2019-01-29 数据结构与算法

7. 数据结构篇：队列

定义

队列和栈一样，是一种操作受限的线性表结构，不同的是栈是后进先出，而队列是先进先出。 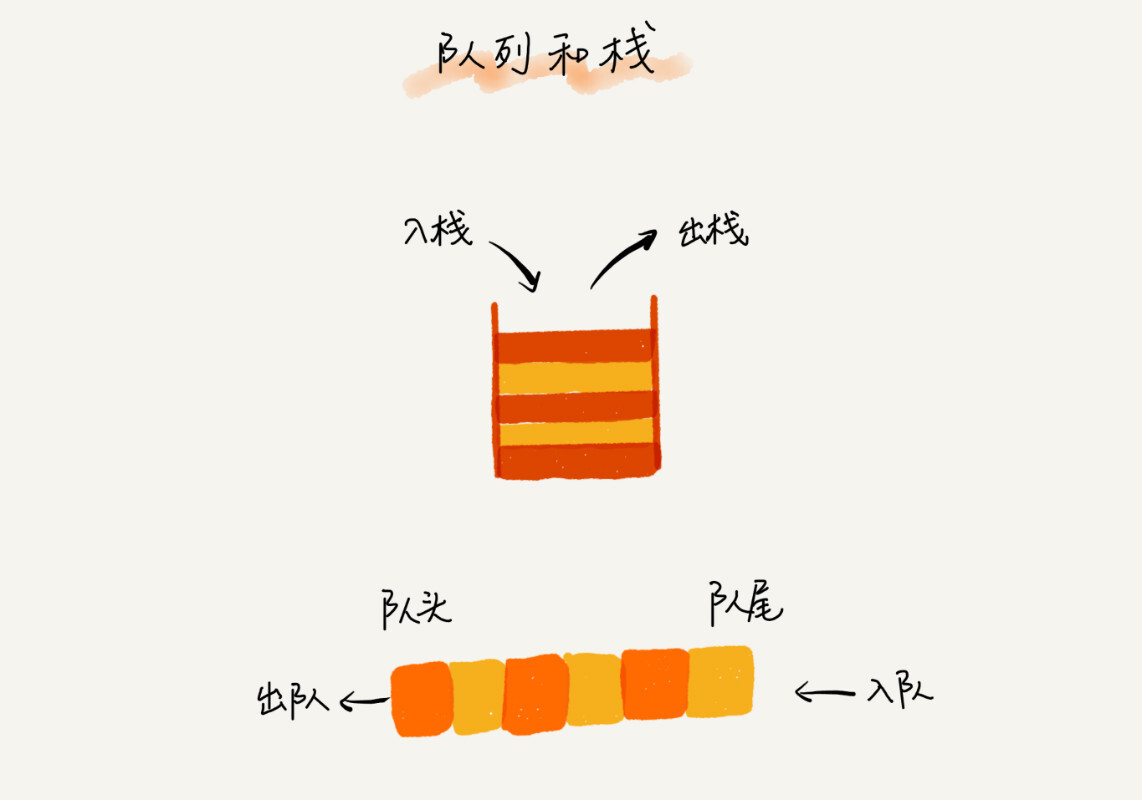image

队列的应用非常广泛，线程次、连接池、消息队列、并发队列等。

顺序队列和链式队列

和栈一样，用数组实现的队列叫顺序队列，用链表实现的队列叫链式队列。

顺序队列

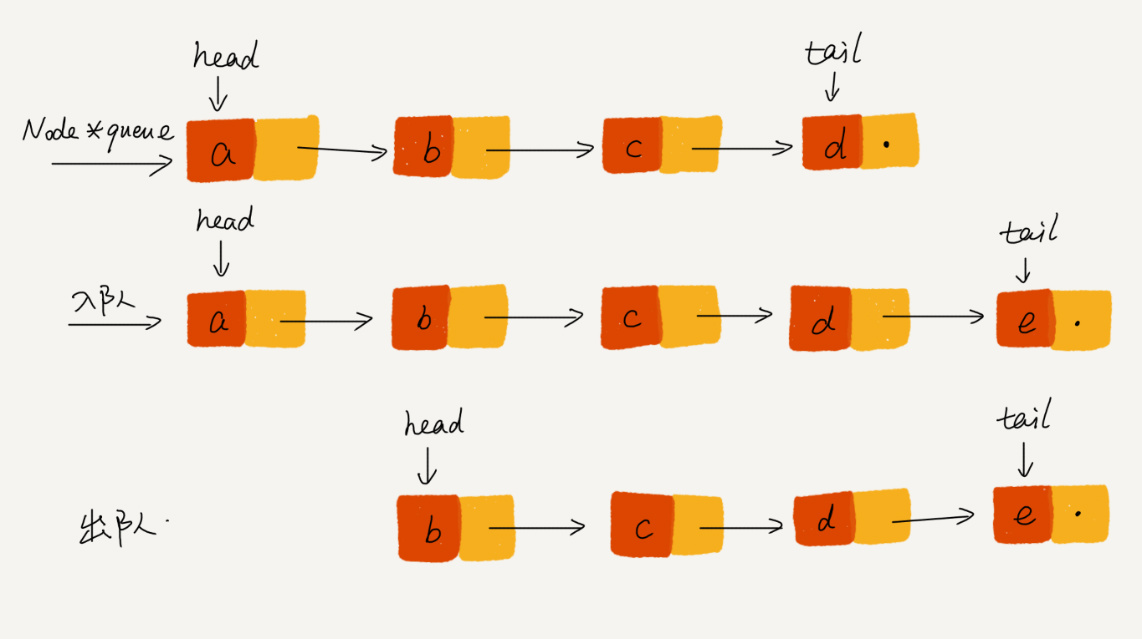
对于栈来说，只需要一个栈顶指针就可以了，而队列需要两个指针：一个 head 指针，指向对头；一个 tail 指针，指向队尾。假设 a, b, c, d依次入队，则 tail指针向后移动，如下图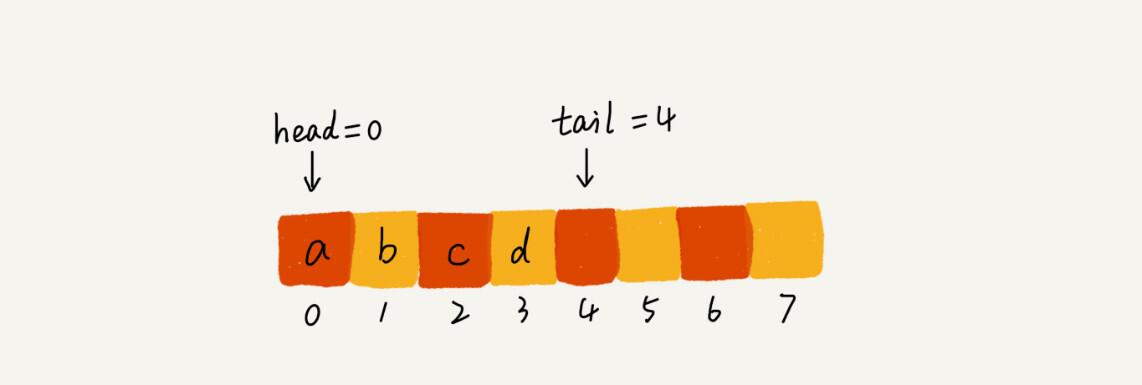： image

当调用 2 次出队操作后，head指针就指向了下标为 2 的位置: 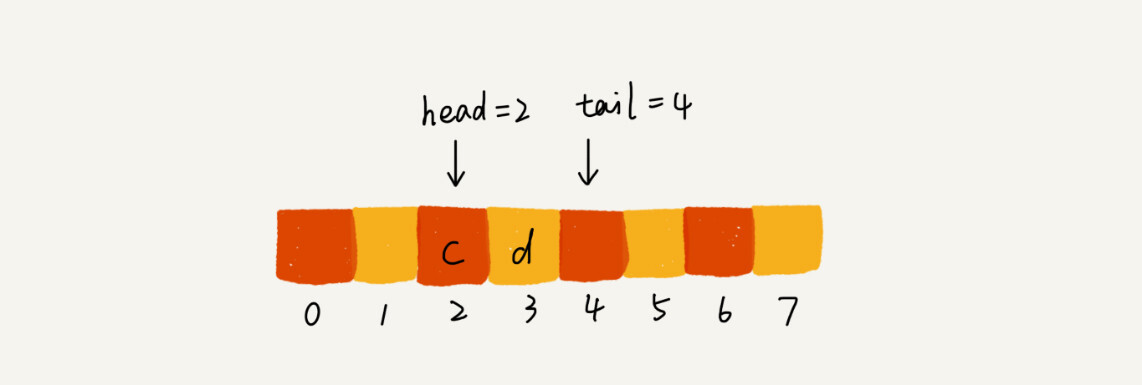image

当 tail 指针移到了最右边，这时候就无法进行入队操作了，这种情况下需要触发一次数据搬移操作，把 head ~ tail之间的数据调整到 0 ~ (tail - head) 的位置。 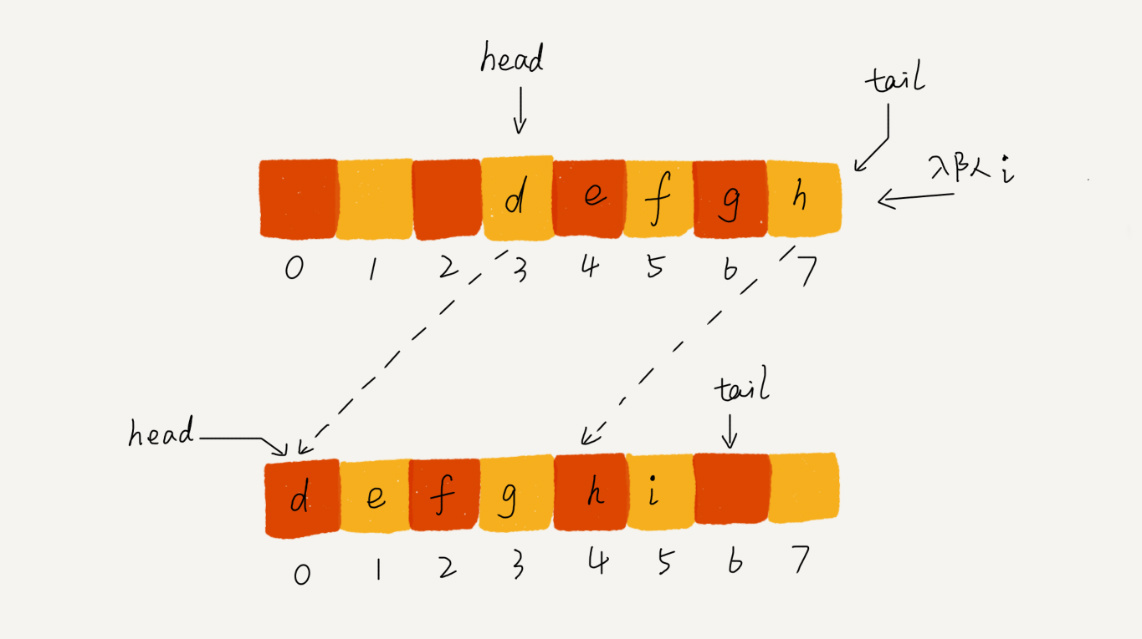image

下面使用数组来实现一个顺序队列：

#!/usr/bin/env python
# -*- coding: utf-8 -*-

class ArrayQueue():
    """顺序队列"""
    def __init__(self, capacity: int):
        self.arr = []
        self.capacity = capacity
        self.head = 0
        self.tail = 0

    def enqueue(self, item):
        if self.tail == self.capacity:
            if self.head == 0:
                print('队列满了')
                return False

            # 进行数据搬移
            for i in range(self.head, self.tail):
                self.arr[i - self.head] = self.arr[i]

            # 重新调整指针和数组
            self.tail = self.tail - self.head
            self.head = 0
            self.arr = self.arr[self.head: self.tail]

        self.arr.append(item)
        self.tail += 1
        print('入队:', item)
        return True

    def dequeue(self):
        if self.head == self.tail:
            print('队列空了')
            return None

        item = self.arr[self.head]
        self.head += 1
        # self.arr = self.arr[self.head:]
        print('出队：', item)
        return item

    def __repr__(self) -> str:
        print('指针：', self.head, self.tail)
        return '{}'.format(self.arr[self.head: self.tail])


if __name__ == '__main__':
    arrayqueue = ArrayQueue(5)
    arrayqueue.enqueue(2)   #入队
    arrayqueue.enqueue(3)
    arrayqueue.enqueue(4)
    arrayqueue.dequeue()    #出队
    arrayqueue.dequeue()    #出队
    arrayqueue.enqueue(5)
    arrayqueue.enqueue(6)
    arrayqueue.enqueue(7)
    arrayqueue.enqueue(8)
    arrayqueue.enqueue(9)   #队列满了，入队失败
    print(arrayqueue)

基于这种思路实现的出队操作时间复杂度为 O(1)，入队操作最好情况时间复杂度为 O(1)，只有在 tail 指针到达尾部时才会触发一次数据搬移操作，这时候时间复杂度为 O(n)，随后进行正常入队，使用摊还分析法思路，均摊时间复杂度就为最好情况时间复杂度 O(1)。

链式队列

基于链表实现同样需要两个指针 head，tail

tail->next = new_node, tail = tail->next    #入队
head = head->next   #出队

image

代码实现：

#!/usr/bin/env python
# -*- coding: utf-8 -*-

class Node:
    def __init__(self, data, next=None):
        self.data = data
        self.next = next

class LinkedQueue:

    def __init__(self):
        self.head = None
        self.tail = None

    def enqueue(self, item):
        new_node = Node(item)
        if self.tail:
            self.tail.next = new_node
        else:
            self.head = new_node
        self.tail = new_node
        return True

    def dequeue(self):
        if self.head:
            item = self.head.data
            self.head = self.head.next
            if not self.head:
                self.tail = None
            return item

    def __repr__(self):
        items = []
        base_node = self.head
        while base_node:
            items.append(base_node.data)
            base_node = base_node.next
        return "->".join(str(item) for item in items)

if __name__ == "__main__":
    q = LinkedQueue()
    for i in range(5):
        q.enqueue(i)
    print(q)    # 0->1->2->3->4

    for _ in range(3):
        q.dequeue()
    print(q)    # 3->4

    q.enqueue("5")
    q.enqueue("6")
    print(q)    # 3->4->5->6

基于链表实现的入对和出队操作的时间复杂度都为 O(1)。

循环队列

在使用数组实现队列的时候，当 tail == n 的时候，会触发数据搬移操作，有没有办法可以避免数据搬移呢？可以使用循环队列这种数据结构来解决。 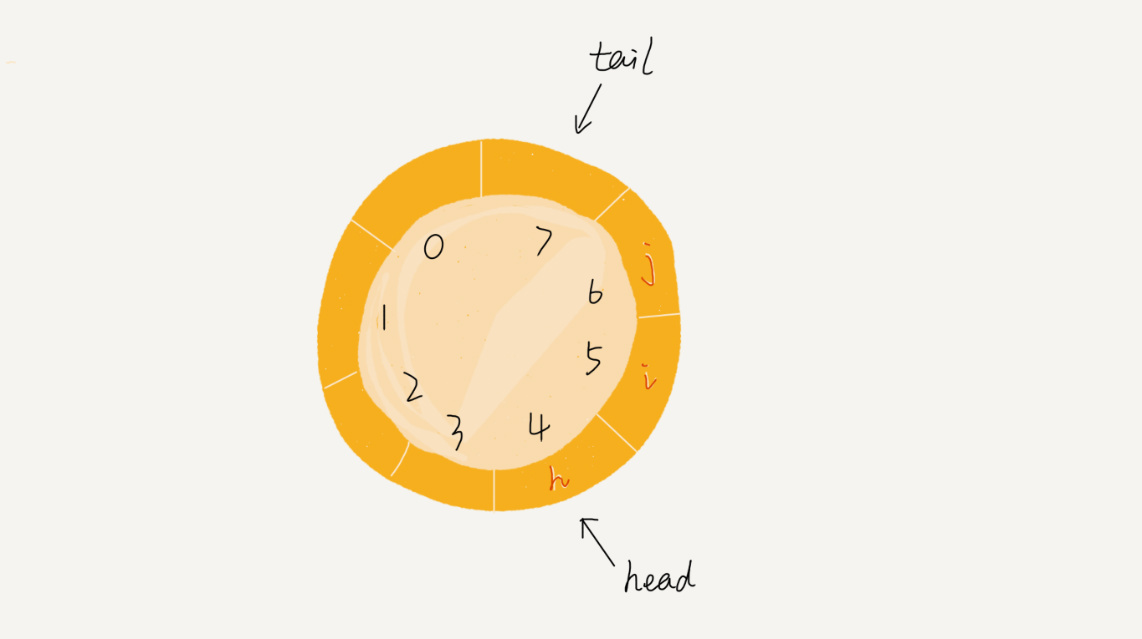image

这个队列的大小为 8，当 tail = 7 时，如果有新的数据 a 入对，则把 tail 指针移到下标 0 的位置，再来一个数据 b，则把 tail 移到下标为 2 的位置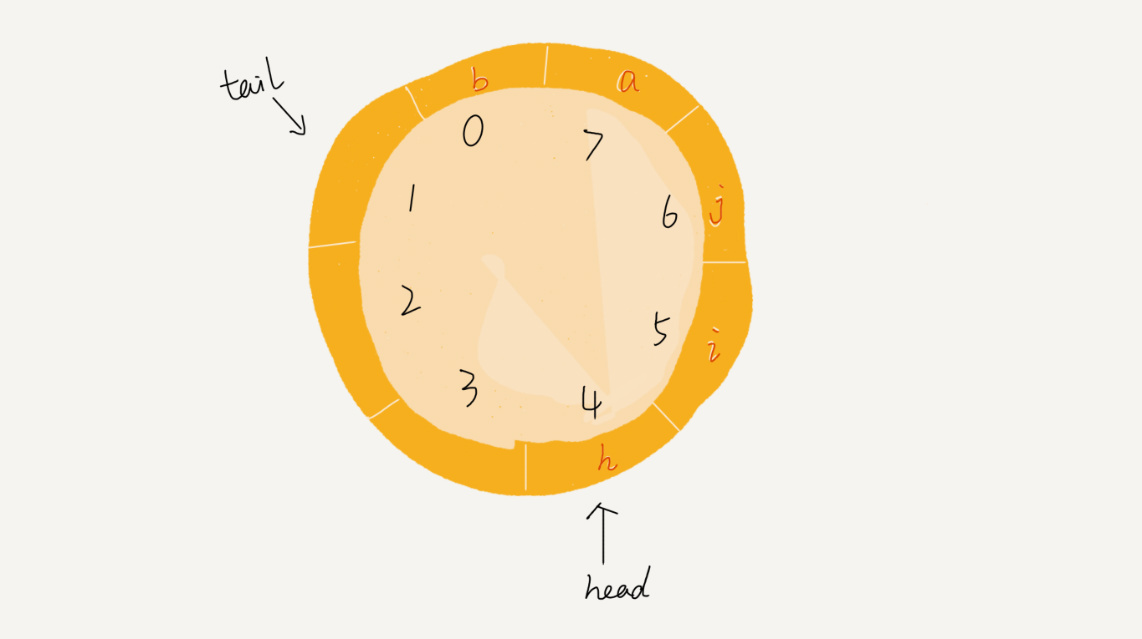： image

看起来很好理解，但实现起来比较难，难点在于判定队空和队满的的条件。看起来队空和队满的条件都是 tail == head，这显然不好判断。

实际上，我们浪费一个存储空间来存储 tail 指针，避免 tail 和 head 重合就好了，像这样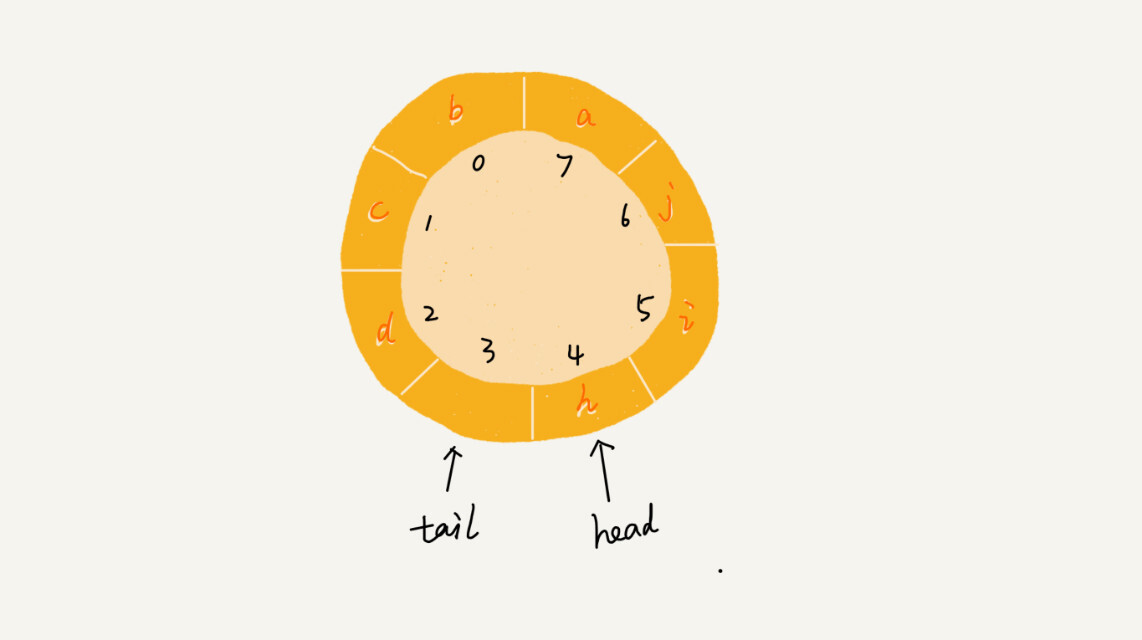： image

这时候队满的条件就是 (tail+1)%n=head。如 tail = 3，n = 8，head = 4，(3+1)%8=4。

代码实现：

#!/usr/bin/env python
# -*- coding: utf-8 -*-

class CircularQueue(object):
    """基于数组实现的循环队列"""
    def __init__(self, capacity):
        self.arr = []
        self.capacity = capacity
        self.head = 0
        self.tail = 0


    def enqueue(self, item):
        n = self.capacity
        if (self.tail + 1)%n == self.head:
            print('队列满了')
            return False
        
        self.arr.append(item)
        self.tail = (self.tail + 1)%n
        return True

    def dequeue(self):
        n = self.capacity
        if self.head == self.tail:
            print('队列空了')
            return False

        item = self.arr[self.head]
        self.head = (self.head + 1)%n
        return item

    def __repr__(self):
        print('指针：', self.head, self.tail)
        if self.head <= self.tail:
            return "{}".format(self.arr[self.head: self.tail])
        else:
            return "{}".format(self.arr[self.head: self.capacity + self.tail])

if __name__ == '__main__':
    Q = CircularQueue(8)
    for i in range(7):  # 实际只能存7个数据，最后一个存tail指针
        Q.enqueue(i)
    print(Q)

    Q.dequeue()
    Q.dequeue()
    Q.dequeue()
    Q.enqueue(7)
    Q.enqueue(8)
    Q.enqueue(9)
    Q.enqueue(10) #入队失败，队列满了
    print(Q)

应用

队列有哪些常见的应用？

1.阻塞队列

1）在队列的基础上增加阻塞操作，就成了阻塞队列。

2）阻塞队列就是在队列为空的时候，从队头取数据会被阻塞，因为此时还没有数据可取，直到队列中有了数据才能返回；如果队列已经满了，那么插入数据的操作就会被阻塞，直到队列中有空闲位置后再插入数据，然后在返回。

3）从上面的定义可以看出这就是一个“生产者-消费者模型”。这种基于阻塞队列实现的“生产者-消费者模型”可以有效地协调生产和消费的速度。当“生产者”生产数据的速度过快，“消费者”来不及消费时，存储数据的队列很快就会满了，这时生产者就阻塞等待，直到“消费者”消费了数据，“生产者”才会被唤醒继续生产。不仅如此，基于阻塞队列，我们还可以通过协调“生产者”和“消费者”的个数，来提高数据处理效率，比如配置几个消费者，来应对一个生产者。

2.并发队列

1）在多线程的情况下，会有多个线程同时操作队列，这时就会存在线程安全问题。能够有效解决线程安全问题的队列就称为并发队列。

2）并发队列简单的实现就是在 enqueue()、dequeue()方法上加锁，但是锁粒度大并发度会比较低，同一时刻仅允许一个存或取操作。

3）实际上，基于数组的循环队列利用 CAS 原子操作，可以实现非常高效的并发队列。这也是循环队列比链式队列应用更加广泛的原因。

3.有限资源池请求排队时的处理

比如线程池、数据库连接池资源的请求。

实际上，在资源有限的场景，当没有空闲资源时，基本上都可以通过“队列”这种数据结构来实现请求排队。

本文首发于 turbobin’s Blog 。转载请注明出处，附上本原文链接， 谢谢合作。

 


关注微信公众账号「曹当家的」，订阅最新文章推送

上一篇:6. 数据结构篇：栈

下一篇:8. 算法篇：递归

All content is licensed under CC BY-NC-SA

Copyright © turbobin's Blog | 2018-2023

Table of Contents