2. 最好、最坏、平均、均摊时间复杂度
上一节掌握了复杂度概念、几种常见类型、以及加法法则,乘法法则已经达到了及格线,但是复杂度分析还不止这点概念。接下来只要掌握了 最好情况复杂度、最坏情况复杂度、平均时间复杂度、均摊时间复杂度 这几个复杂度分析方法,复杂度分析基本就没什么问题了。
最好、最坏情况时间复杂度
我先用 python 来写一段简单代码:
def find(arr, key):
n = len(arr) # n 表示数组长度
pos = -1 # 初始化指针
for i in range(n):
if arr[i] == key:
pos = i
break # 找到就跳出循环
return pos
这是一段在数组中查找指定数据 key 的方法,如果 key 在数组 arr 中,就返回对应的位置,否则返回 -1。我们考虑两种极端的情况:
- 如果 key 在数组中的第一个位置,即 arr[0] == key,循环代码只需要执行一遍,因此时间复杂度为 O(1)。这称为最好时间复杂度,即在最理想的情况下执行这段代码的时间复杂度。
- 如果 key 不在数组中,那么需要遍历完整个数组,最后返回 -1,这时候时间复杂度变成了 O(n),这是最糟糕的情况下执行这段代码的时间复杂度,称为最坏时间复杂度。
平均时间复杂度
还是来分析上面那段代码。 用一点简单的概率学知识来分析,从宏观上来看,要查找的数据要么在数组中,要么不在数组中,假设这两种情况的概率都是 1/2。如果在数组中,那么查找的数据在 0 ~ n-1 任意位置(数组从 0 开始计数)的概率就为 1/2n,考虑每种情况,代码执行的平均时间就为:
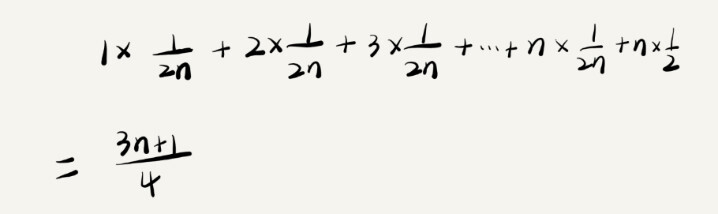
这个值是概念论中的加权平均值,也就叫做期望值。所以平均时间复杂度也叫做加权平均时间复杂度,或期望时间复杂度。 用大 O 表示法,去掉系数和常量,平均时间复杂度是 O(n)。
均摊时间复杂度
均摊时间复杂度,有点像平均时间复杂度,对应的分析方法叫摊还分析法,还是先来看一段代码:
count = 0
arr = [None] * n #初始化一个长度为 n 的数组(为了方便理解先这样表示)
def insert(key):
if count == len(arr):
sum = 0
for i in range(len(arr)):
sum = sum + arr[i]
arr[0] = sum
count = 1
arr[count] = key
count += 1
这是一段往长度为 n 的数组中插入数据的代码,当数组 “满了”之后,遍历一次数组求和,再把和覆盖到数组下标为 0 的位置,再把指针调到下标为 1 的位置。相当于清空一次数组。
很容易看出,最好情况时间复杂度是 O(1),最坏情况时间复杂度是 O(n)。那平均时间复杂度是多少呢?来分析一下:
可以按上面 find 函数的思路来分析,要插入的数据要么在数组中,要么不在数组中,但是,这两种情况的概率还会都是 1/2 吗?显然不是!插入的数据不在数组中的概率在极端的情况下才会出现一次。事实上,可以看做,在 0 ~ n 的位置,这 n + 1 次插入数据的概率都是相同的,为 1/(n+1)。所以加权平均值可以这样表示:
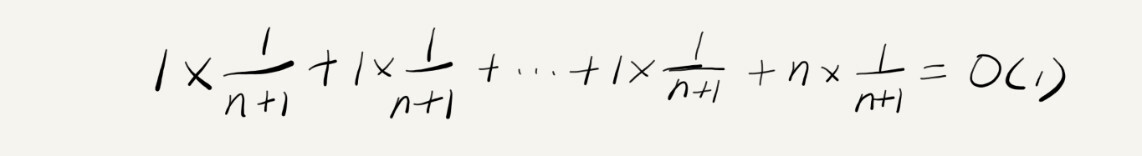
所以平均时间复杂度为 O(1),它和最好情况时间复杂度相等。
看完上面,相信你已经头大了,实际上确实不需要这么复杂,我们引入摊还分析法来分析一下:
上面 insert 操作和 find 操作有很大不同,insert 的操作在大部分的情况下时间复杂度都为 O(1),只有在个别情况下(第 n 次操作)时间复杂度会变为 O(n),而且紧接着第 n + 1 次操作又变回 O(1),那么,整体情况均摊下来,这一组连续的操作均摊时间复杂度就为 O(1)。
这就是摊还分析的大致思路。
一般情况下,均摊时间复杂度,等于最好情况时间复杂度。
本文首发于 turbobin’s Blog 。转载请注明出处,附上本原文链接, 谢谢合作。

关注微信公众账号「曹当家的」,订阅最新文章推送