12. 算法篇:二分查找
二分查找
二分查找过程
- 二分查找针对的是一个有序的数据集合,如果数据是无序的,需要先排序。
- 需要查找的元素 k 每次和区间的中间元素对比,每一次查找将区间缩小为之前的一半,直到找到要查找的元素,或者区间被缩小为0
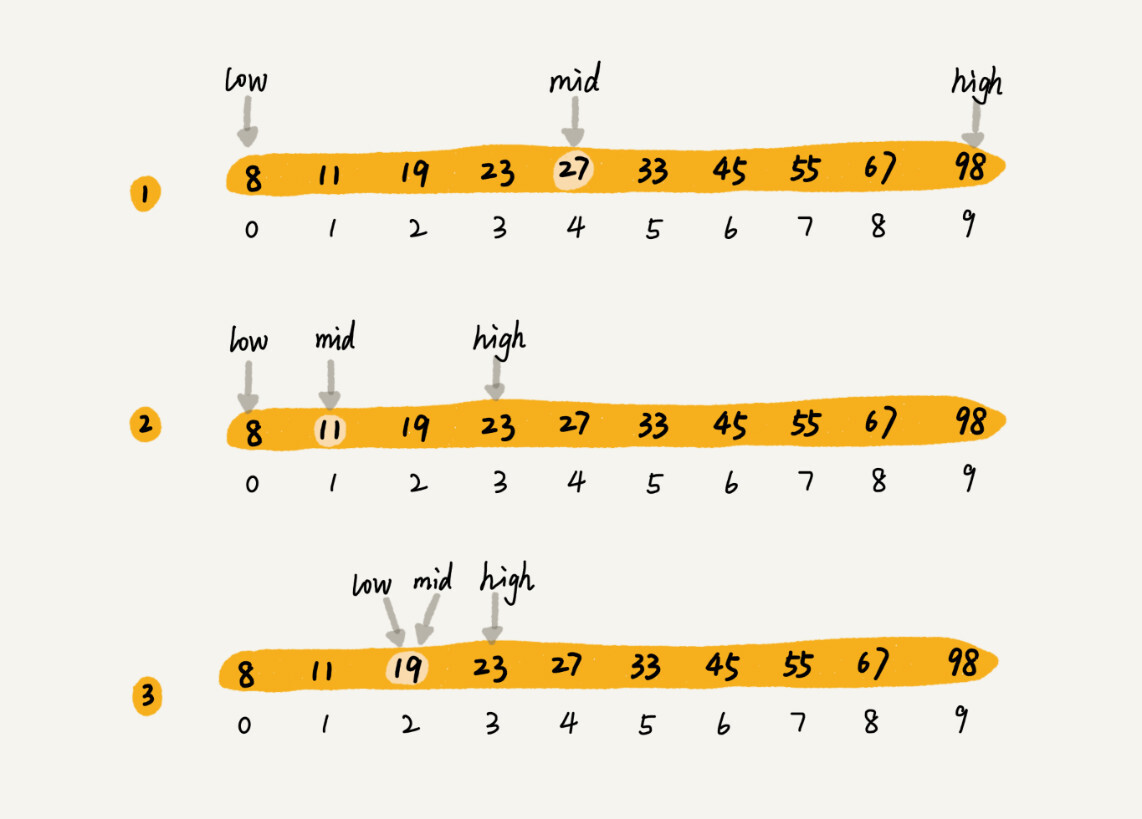
高效的查找速度
假设数据大小为 n,每次查找后数据缩小为原来的一半,直到找到数据,或区间缩小为空才停止

k 是总共缩小的次数,每次只涉及到数据的比较操作,所以时间复杂度为 O(k),当 n/2k=1 时,查找停止,这时 k = logn2n,所以时间复杂度就是 O(logn)。
232 等于 42亿 左右,在其中使用二分查找一个数据,最多只需要比较 32 次。
二分查找的实现
假设数组中不存在重复的元素,二分查找的实现如下。
使用循环过程:
# -*- coding: utf-8 -*-
def binary_search(arr, key):
if len(arr) <= 1:
return 0
min = 0
max = len(arr) - 1
mid = (min + max) // 2 # 地板除,只保留整数
print(mid)
while arr[mid] != key:
if arr[mid] > key:
max = mid - 1
elif arr[mid] < key:
min = mid + 1
mid = (min + max) // 2
if min > max:
return None
return mid
def binary_search2(arr, key):
"""
二分法,时间复杂度 O(logn)
"""
low = 0
high = len(arr) - 1
while low <= high:
mid = (low + high) // 2
if arr[mid] > key:
high = mid - 1
elif arr[mid] < key:
low = mid + 1
else:
return mid
return None
if __name__ == '__main__':
arr = [1, 2, 3, 4, 5]
print('返回数组下标位置:', binary_search(arr, 4))
print('返回数组下标位置:', binary_search2(arr, 8))
注意的点:
- 循环退出条件为 low <= high,而不是 low < high
mid = (low + high) // 2,这种写法实际上有一定的问题,如果 low + high 是一个比较大的值,会导致整型溢出,可以改成low + (hign - low) // 2,或者通过位运算low+((hign-low)>>1)low=mid+1,high=mid-1。如果写成 low=mid 或者 high=mid,有可能会发生死循环。
实际上,二分查找的代码还可以使用递归来实现:
# -*- coding: utf-8 -*-
def binary_search3(arr, key):
n = len(arr)
return _binary_search_recur(arr, 0, n-1, key)
def _binary_search_recur(arr, low, high, key):
if low > high:
return None
mid = low + ((high - low)>>1)
if arr[mid] == key:
return mid
elif arr[mid] < key:
return _binary_search_recur(arr, mid+1, high, key)
else:
return _binary_search_recur(arr, low, mid-1, key)
二分查找的适用范围
- 二分查找依赖的是顺序表结构,也就是数组
- 二分查找的数据集合必须是有序的
- 如果数据量太小,不必要使用二分查找,遍历就好了
- 如果数据量太大,对内存的要求极高,必须使用数组这种连续的内存,如果内存不满足,也无法使用二分查找
二分查找的扩展
查找第一个值等于给定值的元素
给定这样一组数据:[1, 3, 4, 5, 6, 8, 8, 8, 11, 18],查找第一个等于 8 的元素的下标。
对于二分后的值,对于 arr[mid] 大于或小于 key 的情况,遵循一般二分法的处理,对于 arr[mid] == key,需要检查前一个元素是否也等于 key,如果是,需要更新 high = mid - 1。
# -*- coding: utf-8 -*-
"""
二分查找的变体
"""
def binary_search(arr, key):
"""查找第一个值等于给定值的元素"""
n = len(arr)
if n <= 1:
return 0
low = 0
high = n - 1
while low <= high:
mid = low + ((high-low)>>1)
if arr[mid] > key:
high = mid - 1
elif arr[mid] < key:
low = mid + 1
elif (mid == 0) or (arr[mid-1] != key):
return mid
else:
high = mid - 1 # 注意如果少了这行会导致死循环
return None
if __name__ == '__main__':
arr = [1, 3, 4, 5, 6, 8, 8, 8, 11, 18]
print('返回数组下标位置:', binary_search(arr, 8))
查找最后一个值等于给定值的元素
def binary_search(arr, key):
"""查找最后一个值等于给定值的元素"""
n = len(arr)
if n <= 1:
return 0
low = 0
high = n - 1
while low <= high:
mid = low + ((high-low)>>1)
if arr[mid] > key:
high = mid - 1
elif arr[mid] < key:
low = mid + 1
elif (mid == 0) or (arr[mid+1] != key):
return mid
else:
low = mid + 1 # 注意如果少了这行会导致死循环
return None
查找第一个大于等于给定值的元素
def binary_search(arr, key):
"""查找第一个大于等于给定值的元素"""
n = len(arr)
if n <= 1:
return 0
low = 0
high = n - 1
while low <= high:
mid = low + ((high-low)>>1)
if arr[mid] >= key:
if (mid == 0) or (arr[mid-1] != key):
return mid
else:
high = mid - 1
else:
low = mid + 1
return None
查找最后一个小于等于给定值的元素
def binary_search4(arr, key):
"""查找最后一个小于等于给定值的元素"""
n = len(arr)
if n <= 1:
return 0
low = 0
high = n - 1
while low <= high:
mid = low + ((high-low)>>1)
if arr[mid] <= key:
if (mid == n - 1) or (arr[mid+1] != key):
return mid
else:
low = mid + 1
else:
high = mid - 1
return None
快速定位一个 IP 地址的归属地
[202.102.133.0, 202.102.133.255] 山东东营市
[202.102.135.0, 202.102.136.255] 山东烟台
[202.102.156.34, 202.102.157.255] 山东青岛
[202.102.48.0, 202.102.48.255] 江苏宿迁
[202.102.49.15, 202.102.51.251] 江苏泰州
[202.102.56.0, 202.102.56.255] 江苏连云港
IP 地址与归属地的关系被维护成了一个很大的地址库,IP 地址可以转成 32 位整型数值,预先对 IP 地址库进行预处理从小到大排序,于是问题变成了“在有序数组中查找最后一个小于等于某个给定值的元素”。
当要查找某个 IP 归属地时,我们使用二分查找法,找到最后一个起始 IP 小于等于这个 IP 的区间,然后检查这个 IP 是否在这个 IP 区间内,如果在就取出对应的归属地显示,如果不在就返回未查找到。

关注微信公众账号「曹当家的」,订阅最新文章推送