9. 算法篇：排序（上）

如何分析一个排序算法

排序算法的效率

1.最好、最坏。平均时间复杂度

2.时间复杂度的系数、常数、低阶

当数据规模小时，需要分析时间复杂度的系数、常数、低阶。

3.比较次数、交换（移动）次数

排序的时候都会涉及到两种操作：比较，交换（移动）。
因此需要将比较和交换（移动）的次数考虑进去

排序算法的内存消耗

内存消耗可以通过空间复杂度来衡量。

原地排序：指空间复杂度为 O(1) 的排序算法，如冒泡排序、插入排序、选择排序

排序算法的稳定性

稳定性指的是：如果待排序的序列中如果有相等的元素，经过排序后，相等的元素前后顺序不变（不会交换位置）。

比如对订单排序，订单有金额，下单时间属性，如果要求对订单按照金额大小排序，相同的金额按照下单时间先后排序。

如果先对金额进行排序，再对金额相同的订单按照下单时间局部排序，实现起来很复杂。

正确的思路是，先对订单按照下单时间先后排序，再对金额大小进行排序。第二次排序用的是稳定算法排序，所以订单时间顺序不会变。

冒泡排序

实现原理比较简单： 这种情况，实现的时间复杂度是 O(n²)。

实际上，这个过程还可以优化，如果原有的序列已经是有序的，那么只需要执行一次冒泡操作就可以了，如果判断没有发生数据交换，则可以断定这个序列已经是有序的。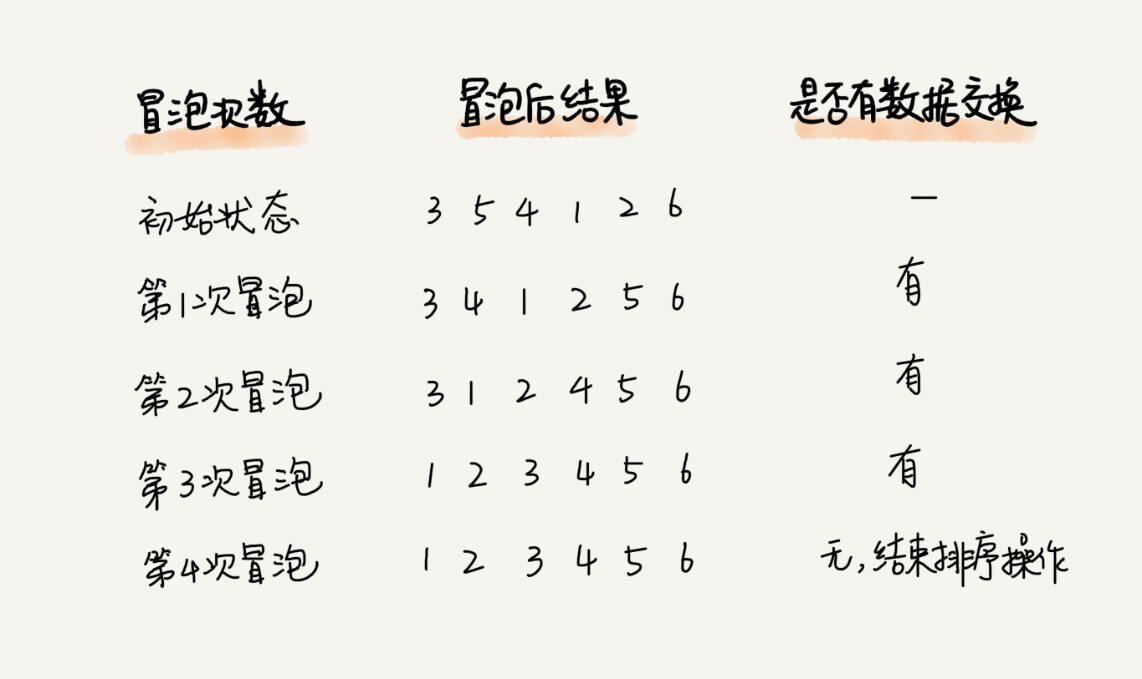

def bubbo_sort(arr):
    n = len(arr)
    if n <= 1:
        return arr

    flag = False    #提前退出冒泡排序的标志
    for i in range(n-1):
        for j in range(n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
                flag = True

        if not flag:    #表示没有数据交换
            break
    return arr

arr = [4, 5, 6, 1, 2, 3]
arr = bubbo_sort(arr)
print(arr)

分析三点：

• 冒泡排序只涉及相邻数据的交换，所以它的空间复杂度是 O(1)，是一个原地排序算法。
• 当有两个相同元素时，不会交换顺序，因此冒泡排序是稳定的排序算法
• 冒泡排序最好情况时间复杂度是 O(n)，最坏情况时间复杂度是 O(n²)，平均情况时间复杂度分析有些复杂，答案是 O(n²)。

插入排序

思想是：从未排序区间取元素插入到已排序区间合适的位置，初始序列已排序区间就是第一个元素。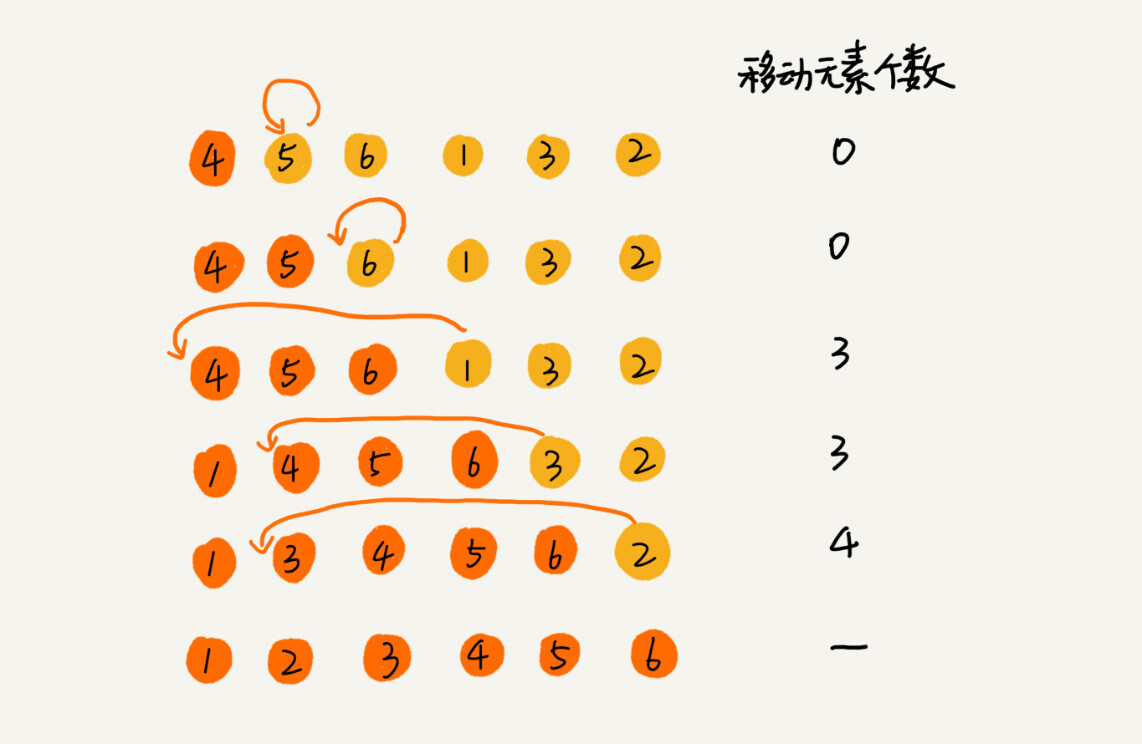

代码实现：

def insert_sort(arr):
    n = len(arr)
    if n <= 1:
        return arr

    for i in range(1, n):
        value = arr[i]
        j = i - 1
        while j >= 0:
            if arr[j] > value:
                arr[j+1] = arr[j]
                j -= 1
            else:
                break
        arr[j+1] = value

    return arr

arr = [4, 5, 6, 1, 2, 3]
arr = insert_sort(arr)
print(arr)

分析三点：

• 插入排序不需要额外的存储空间，所以它的空间复杂度是 O(1)，是一个原地排序算法。
• 当有两个相同元素时，不会交换顺序，因此插入排序是稳定的排序算法
• 插入排序最好情况时间复杂度是 O(n)，最坏情况时间复杂度是 O(n²)，平均情况时间复杂度相当于在数组中插入一个元素，涉及到数据的搬移，参看数组一节，插入数据的平均时间复杂度是 O(n)，循环 n 次插入操作，故平均时间复杂度是 O(n²)。

选择排序

有点类似插入排序，也分已排区间和未排区间。但是选择排序每次会从未排序区间找到最小的元素放到已排序区间的末尾。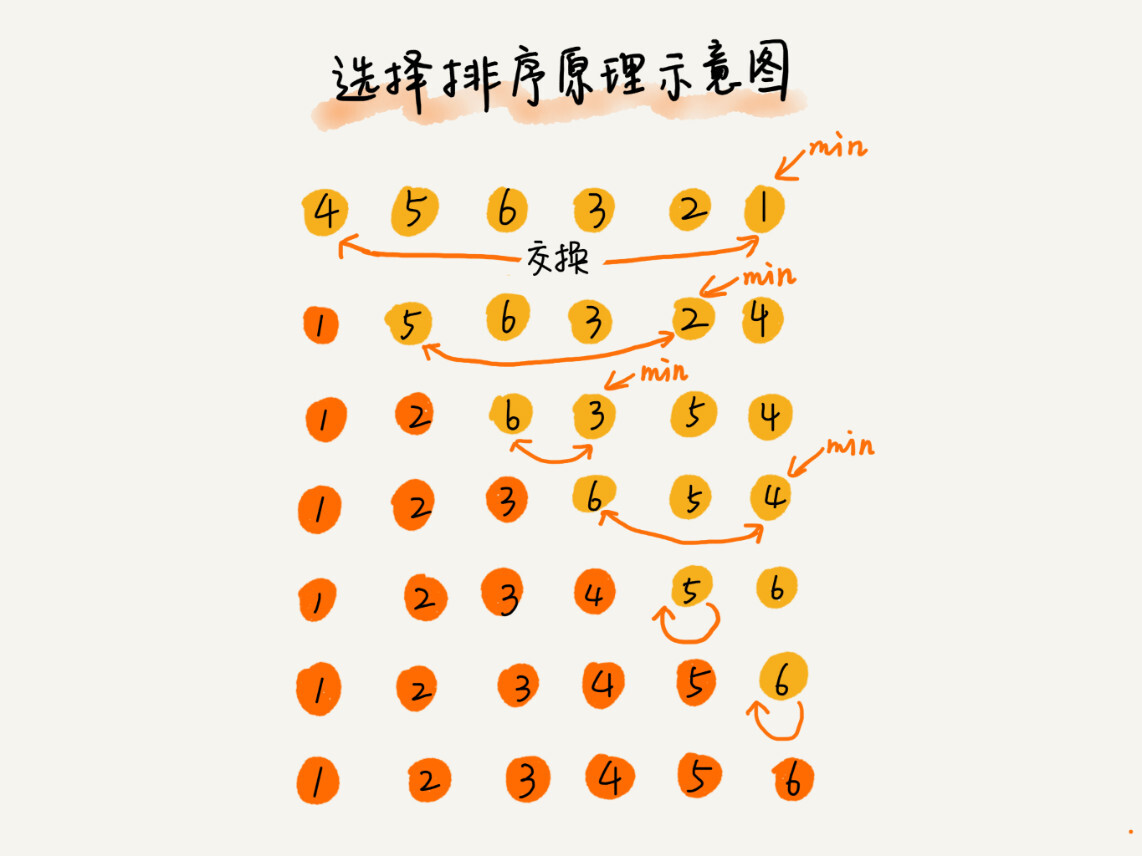

代码实现：

def findmin(arr):
    """
    找出数组中最小值
    """
    min_num = arr[0]
    min_index = 0
    n = len(arr)
    for i in range(1, n):
        if arr[i] < min_num:
            min_num = arr[i]
            min_index = i

    return min_index


def select_sort(arr):
    """
    快速排序，时间复杂度 O(n^2)
    """
    new_arr = []
    for i in range(len(arr)):
        min_index = findmin(arr)
        new_arr.append(arr.pop(min_index))

    return new_arr


arr = [3, 5, 1, 6, 0, 6]
# print(findmin(arr))
print(select_sort(arr))

上面代码为了方便理解，我申请了额外的存储空间，没有用原地排序算法，实际上，可以改进一下：

# 选择排序
def selection_sort(arr):
    n = len(arr)
    if n <= 1:
        return arr

    for i in range(n):
        min_index = i
        min_val = arr[i]
        for j in range(i, n):
            if arr[j] < min_val:
                min_val = arr[j]
                min_index = j
        arr[i], arr[min_index] = arr[min_index], arr[i]

    return arr

很容易看出，选择排序最好、最坏、平均时间复杂度都为 O(n²)。

值得注意的是，选择排序并不是稳定的排序算法，排序之后相同的元素会交换前后顺序。

总结

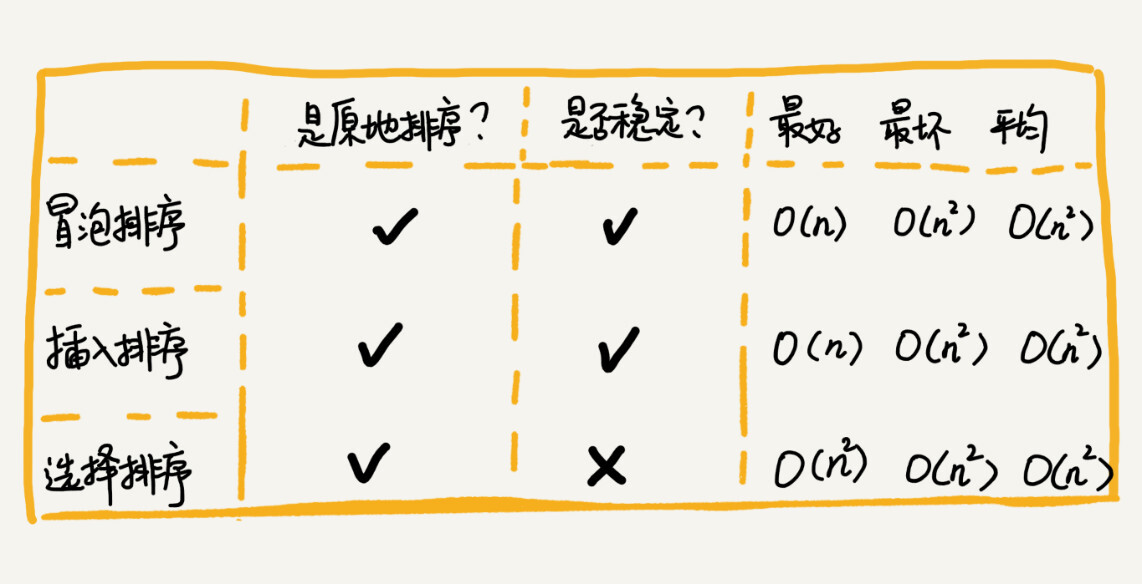
三种排序算法的性能对比：

插入排序 > 冒泡排序 > 选择排序

本文首发于 turbobin’s Blog 。转载请注明出处，附上本原文链接， 谢谢合作。

 

关注微信公众账号「曹当家的」，订阅最新文章推送