17. 数据结构篇：红黑树

平衡二叉查找树

平衡二叉树定义：二叉树中任意一个节点的左右子树的高度相差不能大于1。

完全二叉树和满二叉树都属于平衡二叉树。

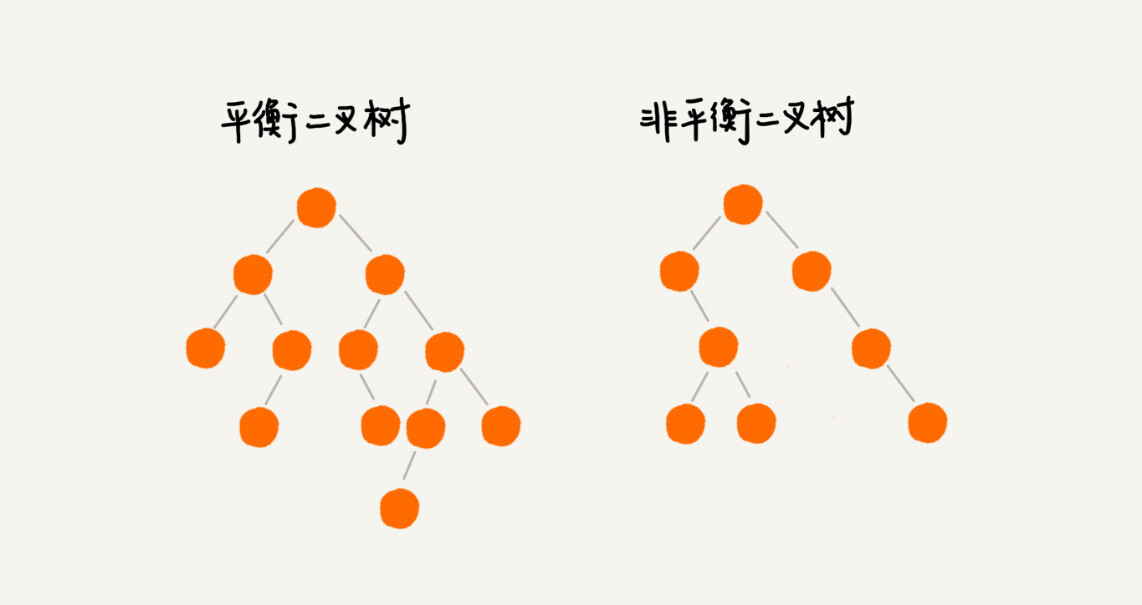
AVL 树 是最早被发明的平衡二叉查找树，它的任何节点的左右子树的高度相差不超过 1，是一种高度平衡的二叉查找树。它的平均和最坏情况下的时间复杂度都是 O(logn)。

AVL 树的插入和删除操作可能需要通过一次或多次的树旋转来重新实现树的平衡。

红黑树

红黑树(R-B Tree) 是一种不严格的平衡二叉查找树，它的节点一类被标记为黑色、一类被标记为红色，它需要满足以下几个要求：

• 根节点是黑色的。
• 每个叶子节点都是黑色的空节点(null)，也就是说，叶子节点不存储数据。
• 任何相邻的节点不能同时为红色，也就是说，红色节点是被黑色节点隔开的。
• 每个节点，从该节点到达其可达子节点的所有路径，都包含相同数目的黑色节点。

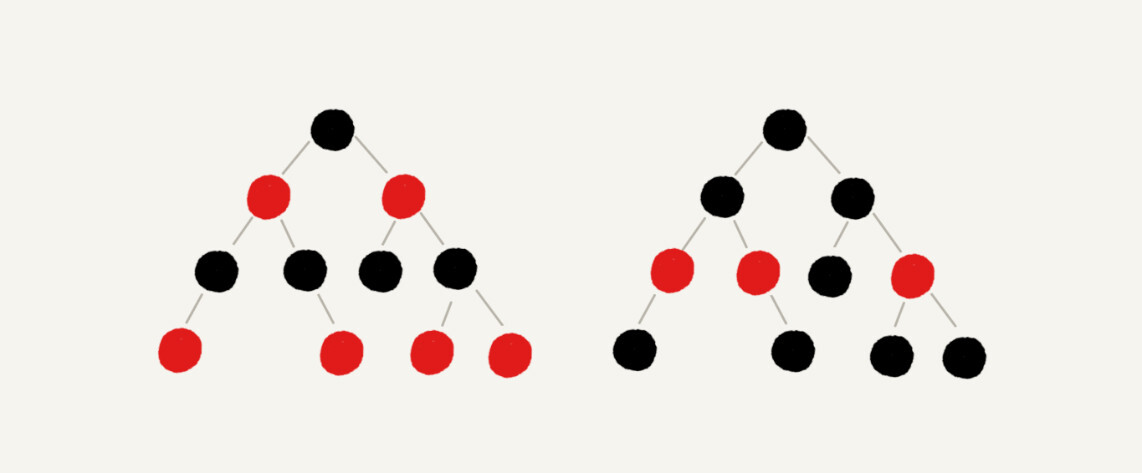
红黑树的插入、删除、查找各种操作性能都比较稳定，时间复杂度为 O(logn)， 而且在维护平衡的成本上要比 AVL 树要低。因此得到了更广泛的应用。

红黑树的平衡调整

左旋和右旋

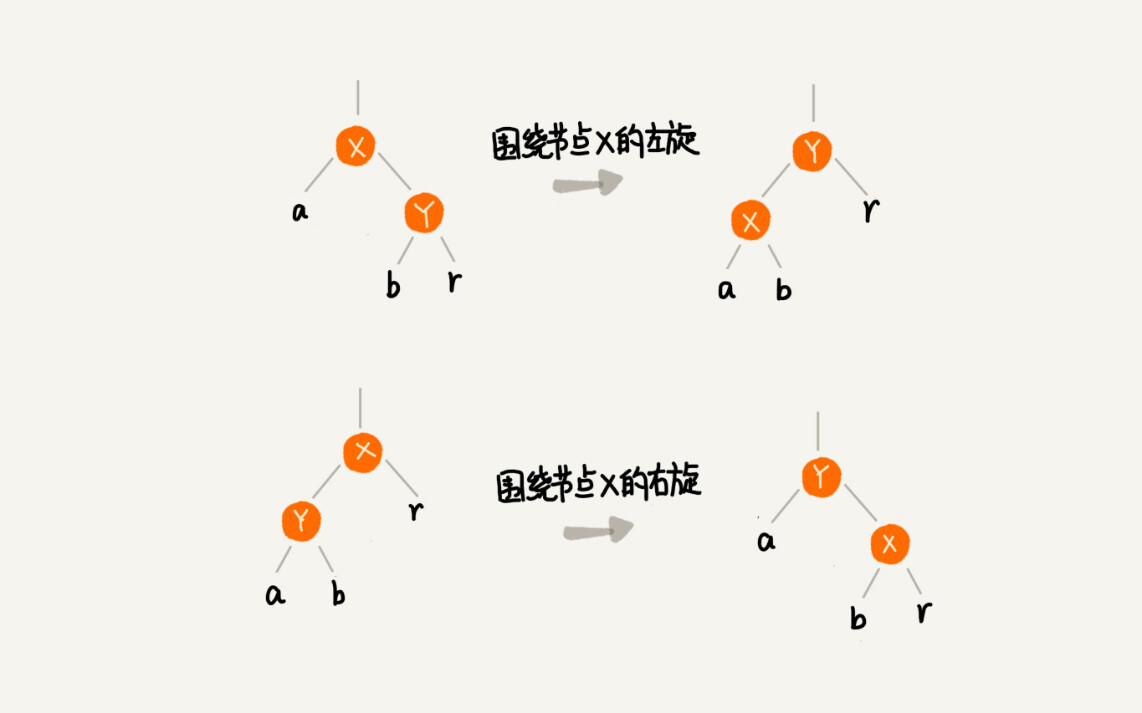
插入时的平衡调整

红黑树规定，插入的节点必须是红色的。而且，二叉查找树中新插入的节点都是放在叶子节点上。

红黑树的调整过程包含两个基础的操作：左右旋转和改变颜色。

 

关注微信公众账号「曹当家的」，订阅最新文章推送